ChemVizOverview |
Overview of Quantum Chemistry |
| Quantum Chemistry Overview Materials
Readings Lab Activities Support Materials Related Links Developers' Tools
|
How Much Do I Already Know?Key Points
OverviewThis section provides a very rough review of the quantum chemistry needed to continue in this program. There are a number of good on-line reviews, my favorite being the materials developed by David Sherrill at the Center for Computational Quantum Chemistry. An additional, but slow (heavy use of GIF files), is entitled "Quantum Mechanics" at the Wilson Institute, University of California, San Diego.There are basically two different models of atomic structure, the Bohr model and the quantum model. In both models, we are often interested in evaluating the energy of a particular system. Bohr Model:Electrons are "particles" that revolve around the nucleus in orbits. These orbits are at fixed distances from the nucleus. Electrons can move between orbits, using or releasing energy in the process.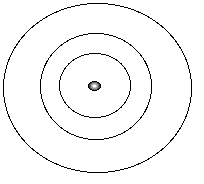
 where
n = quantum number (orbit number) 
Quantum Model:The quantum model says that electrons are not particles, but have wavelike characteristics. It uses the Schroëdinger's equation to calculate various properties of the electrons.
The Schroëdinger's Equation: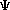 = E = E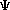 where:
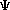 = psi, the wavefunction = psi, the wavefunctionE = the energy of the sytem H = The "Hamiltonian", a nasty mathematical operator. The Hamiltonian equation is shown below.
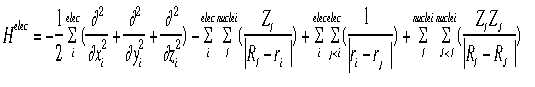 The hamiltonian shown in the graphic above is the hamiltonian for the electrons. Notice that there are four terms (each term separated by a "+" or "-" sign):
Schroëdinger's equation is an eigenvalue equation. From it we obtain two interesting
and important values: E, the energy of the system, and As an example of what these wavefunctions look like, the graphic below shows the mathematical equations to calculate the wavefunctions for a one-electron system -- hydrogen -- at the level of the 1s, 2s, and 2p orbitals:
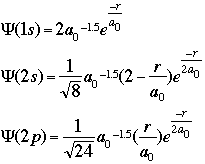 The important terms in these equations are the radius of the electron from the nucleus and the constant known as the Bohr radius, a value of 0.529 angstroms, or 0.528 Å. As an enrichment activity, you might consider modeling these equations using a simple spreadsheet or equation-solver such as MathCAD. The graphic below shows a section of my spreadsheet. I used a Bohr radius of 52.9 picometers, with the electron radius increasing by increments of 2 pm. If you graph the probabilities as a function of the radius, as shown below, you should see that the electron has the highest probability of being found at the "nodes" where Bohr predicted the orbitals should be:
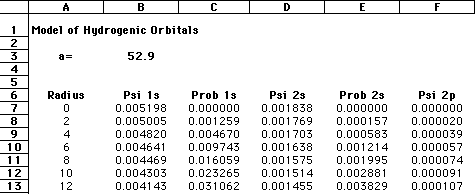
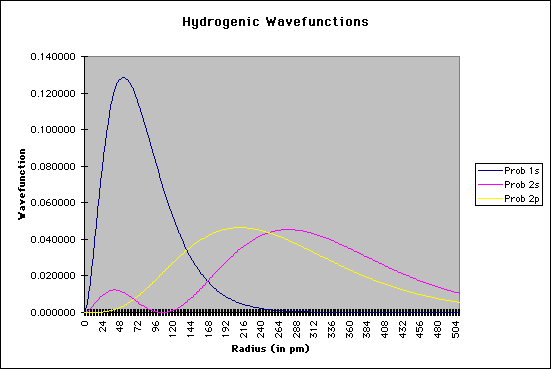 Needless to say, calculating Schroëdinger's equation for systems with more than one electron is quite difficult. However, by using a number of approximations, coupled with the ever-increasing number-crunching of modern computers, it is now possible to "solve" Schroëdinger's equation for multiple-electron systems. |
in cooperation with the
National Center for Supercomputing Applications
© Copyright 1999-2000 The Shodor Education Foundation, Inc.