ChemViz

In order to be able to solve Schroëdinger's equation for any system larger than an atom with one electron, various approximations need to be made. Each of these approximations contributes its own inaccuracies to the final result, which must be accounted for in reporting results. One of the more important approximations used is the Born-Oppenheimer approximation.

The Born-Oppenheimer approximation is the first of several approximations made when trying to solve Schroëdinger's equation for more complex systems than one or two electrons. It separates electron and nuclear motion based on the idea that nuclear mass is so much larger than electron mass that the nuclei are basically "fixed" particles. Electrons react instanteously to changes in the position of the nuclei. This equation shows the full Hamiltonian for a molecular system.

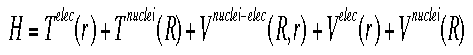Shown below is the equation for the "electronic" Hamiltonian (one that neglects the kinetic energy term for the nuclei).

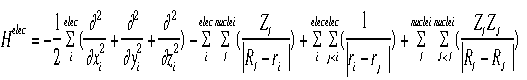Below is the Hamiltonian used in the Schroëdinger equation describing the motion of electrons in a field of fixed nuclei, shown in the first equation.

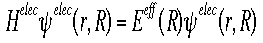Solving this equation for the electronic wavefunction will produce E_eff, the effective nuclear potential function.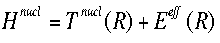

E_eff is used as the potential for the nuclear Hamiltonian. This Hamiltonian is used for nuclear motion, describing the vibrational, rotational, and translational states of the nuclei.

Developed by

The Shodor Education Foundation, Inc.
in cooperation with the
National Center for Supercomputing Applications

ChemViz

Overview

Overview of the Born-Oppenheimer Approximation

How Much Do I Already Know?

Key Points

Overview