ChemVizOverview |
Bohr Radius |
| Bohr Radius Overview Materials
Readings Lab Activities Support Materials Developers' Tools Related Links |
Bohr, a scientist, was trying to understand why atoms do not collapse, as well
as understand the various aspects of experimental spectra and the nature of
light. Using Rydberg's equation which described the frequencies in a
spectrum, Bohr was looking to understand atomic structure using the principles
of classical theories of physics. The first issue is determining total energy in classical mechanics. Classical mechanics suggests that for a charged particle (in this case, the electron) orbiting an oppositely-charged particle (the nucleus). Rutherford developed the equation:
 The angular momentum (omega) is defined as the velocity v divided by the radius r, so the equation becomes:
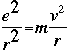 The total energy of any system is defined as:
The equation for potential energy is:
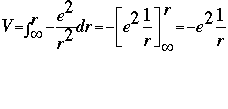 Kinetic energy is expressed in the classical form:
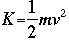 The equation for the Coulomb (centripetal) force is:
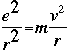 We can rewrite this equation:
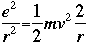 The total energy W is now:
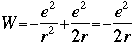 One of the ideas generated by Bohr and others was to compare this equation with the equation that describes total energy in the then-fledgling quantum theory:
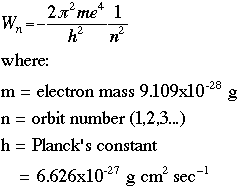 The following graphic derives the value of the radius r by setting the quantum energy equation equal to the classical energy equation:
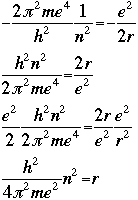 For the first orbit where n=1, the radius r is called the Bohr radius, and is symbolized as a0:
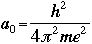
|
in cooperation with the
National Center for Supercomputing Applications
Copyright © 1999