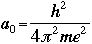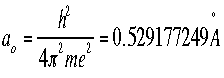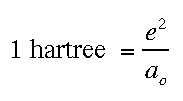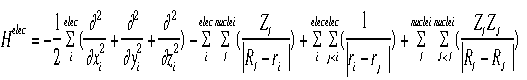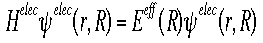|
Home
Key Points
Overview Materials
Computational Science
Computational Chemistry
Basic Quantum Chemistry
Schrodinger's Equation
Atomic Units
The Born Oppenheimer Approximation
The Hartree Fock Approximation
Key Points
Readings
Overview
Atomic Orbitals
Lab Activities
Z-matrices
Basis Sets
Geometry Optimizations
Ionization Energies
Support Materials
Interactive Tools
Glossary of Terms
Quick Guide to DISCO Output File
Related Links
ChemViz
Computational Chemistry
SUCCEED's Computational Chemistry Developers' Tools
What's New?
Discussion Board
Team Members
Email the Group
Contact Webmaster
|
Computational Science
- Scientific Research can be classified into four main categories:
- Observational Science
- Experimental Science
- Theoretical Science
- Computational Science
- Computational Science uses everything that scientists already know about a
problem and incorporates it into a mathematical problem which can be
solved. The mathematical model which then develops gives scientists more
information about the problem.
- Computational Science is beneficial for to main reasons:
- It is a cheaper method of conducting experiments.
- It provides scientists with extra information which helps them to better
plan and hypothesize about experiments.
Computational Chemistry
- Computational chemistry is a branch of chemistry that generates data,
which complements experimental data on the structures, properties and
reactions of substances. The calculations are based primarily on
Schroedinger's equation.
- Computational chemistry is particularly useful for determining molecular
properties which are inaccessible experimentally and for interpreting
experimental data
- With computational chemistry, you can calculate:
- electronic structure determinations
- geometry optimizations
- frequency calculations
- transition structures
- protein calculations, i.e. docking
- electron and charge distributions
- potential energy surfaces (PES)
- rate constants for chemical reactions (kinetics)
- thermodynamic calculations- heat of reactions, energy of activation
- There are three main types of calculations:
- Ab Initio: (Latin for "from scratch") a group of methods in which
molecular structures can be calculated using nothing but the
Schroedinger equation, the values of the fundamental constants and the
atomic numbers of the atoms present (Atkins, 1991).
- Semi-empirical: techniques use approximations from empirical
(experimental) data to provide the input into the mathematical models.
- Molecular mechanics: uses classical physics to explain and
interpret the behavior of atoms and molecules
Basic Quantum Chemistry
- Bohr model states that electrons are particles which move around the
nucleus in fixed orbitals.
- Electrons need a certain amount of energy to move between orbitals. The
equation to find the amount of energy needed is:

- Quantum model states that electrons are not particles, but have wavelike
characteristics and so do not move in uniform orbitals.
- Various properties of the electrons can be calculated with the
Schroëdinger's Equation:
H
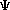 = E = E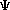
- Bohr's radius is an important constant in the Schroëdinger's
Equation. In an atom, for the first orbit where n=1, the radius r is called
the Bohr radius, and is symbolized as a0:
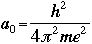
Schroëdinger's Equation
Atomic Units
The Born Oppenheimer Approximation
- This approximation helps in finding the Schroëdinger's Equation for
large systems. It is an equation describing the motion of one electron
assuming the nucleus is not moving. (False assumption, but helps in
simplifying equation.)
- Shown below is the equation for the "electronic" Hamiltonian (one that
neglects the kinetic energy term for the nuclei).
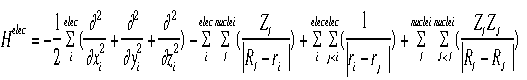
- Below is the Hamiltonian used in the Schroëdinger equation describing
the motion of electrons in a field of fixed nuclei, shown in the first
equation
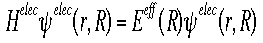
- This Hamiltonian is used for nuclear motion, describing the vibrational,
rotational, and translational states of the nuclei.
The Hartree Fock Approximation
The Hartree Fock Approximation is what is known as a Self-Consistent Field Method (SCF).
The Method:
- begin with a set of approximate orbitals for all the electrons in the system
- one electron is selected, and the potential in which it moves is
calculated by freezing the distribution of all the other electrons and
treating their averaged distribution as the centrosymmetric source of potential
- the Schrodinger equation is solved for this potential, which gives a new orbital for it
- the procedure is repeated for all the other electrons in the system, using
the electrons in the frozen orbitals as the source of the potential
- at the end of one cycle, there are new orbitals from the original set
- the process is repeated until there is little or no change in the orbitals
Things to keep in mind:
- defined as the wavefunction of an electron in an atom
- square of the AO gives the probability density
- any electron described by an orbital is said to occupy that orbital
- atomic orbitals have a well-defined significance only for hydrogenic atoms
- hydrogenic atoms are used in many of the computational approximations
- the orbital is a mathematical expression, describing the probability of
finding an electron at some point near the nucleus
|

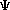 = E
= E