ChemVizOverview |
Overview of Computational Science |
| Computational Science Overview Materials
Readings Lab Activities Support Materials Related Links Developers' Tools
|
How Much Do I Already Know?Key Points
OverviewIt has been suggested that if aircraft technology had advanced at the same rate as that of computer technology, it would be possible to get on a Boeing 747 that would be large enough to carry 12,000 people to the moon in about three hours for the round-trip cost of about twelve dollars. Computer technology, particularly in the areas of increased speed of calculations and more efficient memory storage devices, has improved at a whirlwind pace over the past 20 years. Many of the improvements in computer hardware and in the algorithms (software) that control computers have presented a new tool for investigating scientific problems. Scientific research can be categorized in three areas:
A fourth and new area of scientific research has emerged over the past 20 or 30 years that is revolutionizing how scientists work and how they think about doing science. Computational science is the application of computational and numerical techniques to solve large and complex problems. Computational science takes advantage of not only the improvements in computer hardware, but probably more importantly, the improvements in computer algorithms and mathematical techniques. Computational science allows us to do things that were previously too difficult to do due to the complexity of the mathematics, the large number of calculations involved, or a combination of the two. Computational science also allows us to build models that allow us to make predictions of what might happen in the lab, so that we are perhaps better prepared to make good observations or to understand better what we are seeing. We can also use computational techniques to perform experiments that might be too expensive or too dangerous to do in the lab. We can, for example, use computational techniques to predict how a new drug might behave in the body. This allows us to reduce, but not eliminate, the number of animal tests that we might have done prior to the development of computational pharmacology techniques. While computational models cannot replace the lab, they have certainly become an intricate part of the overall search for scientific knowledge. There are many definitions of computational science -- most of them describe it as "an interdisciplinary approach to the solution of complex problems that uses concepts and skills from the disciplines of science, computer science, and mathematics". Of considerable importance is your understanding that the study of computational science is not computer science -- computational science is a methodology that allows the study of various phenomenon. We consider computational science to be a fourth method of doing research, an addition to observational, experimental, and theoretical methods:
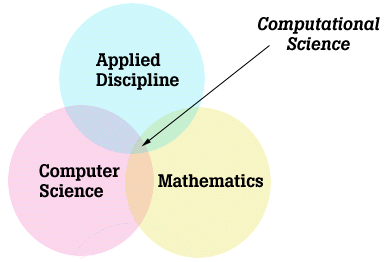
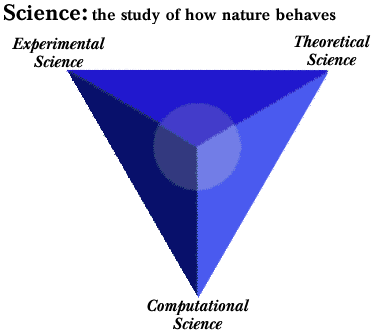 As the graphic above shows, science is defined as the study of how nature behaves. The three supporting sciences are theoretical, experimental, and computational. There is clearly a "symbiotic" relationship between the three -- theoretical findings "drive" the experimentalists, experimental data is used to build and validate computational research, computational research provides the theorists with new directions and ideas. Many of the fundamental questions in science (especially those with potentially broad social, political, and scientific impact) are sometimes referred to as "Grand Challenge" problems. Many of the the Grand Challenge problems are those that can only be solved computationally. Certainly chemistry problems are considered by all computational scientists to be one of the major grand challenge categories. In chemistry, the argument has been made that we have known (since 1928) all of the theoretical mathematics needed to solve every chemical problem. It is only since the birth of computational science (late 1950's) that we have had the tools and technologies needed to solve these complex mathematical equations born from the theorists. There are other ways to look at computational science. Some folks will describe it as the intersection of three disciplines:
 We use a slightly different, less discipline-specific picture of computational science: application, algorithm, and architechture:
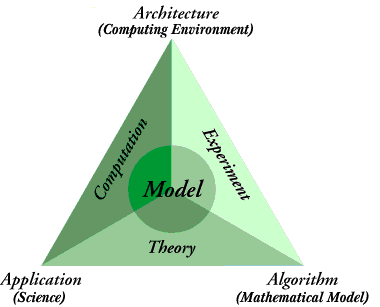 In this view, computational science is a scientific endeavor (application) that is supported by the concepts and skills of mathematics (algorithms) and computer science (architecture). Central to any computational science problem is the science itself -- what scientific event or problem is of interest? What are its boundaries, what components or factors are part of the system, what assumptions can be made about its behavior, what do we know about other systems that has some similarity to the one we are interested in studying? Once these key decisions have been made, then the search begins for a suitable algorithm: a mathematical model that can be created to represent the behavior described by the parameters of the problem. Often we need to use one or several numerical "recipes" to begin the solution of the mathematical model generated. Many numerical recipes are too complex to calculate by hand and/or require repetitive calculations -- iterations -- to get close to an answer. At this point we can use the technologies of computer science to implement our algorithm or mathematical model on some suitable sized computer using some computational software tool. Needless to say, this whole process is itsef "iterative" -- solutions to preliminary algorithmic approaches to the problem generate a better algorithm, perhaps with the need for increasing computational power and/or precision. Perhaps a simple problem is helpful. This problem is chosen as an example since it is something that everyone will certainly understand. The application or problem that I am interested in studying is that of tying my shoe! I wish to develop a computational solution to the physical event of tying my shoe. Since this is a phenomenon that is well understood, we don't have to spend too much time thinking about the science of it, we can proceed fairly directly to developing an algorithm for the problem. We begin this process by declaring each lace of the shoestring to have some length A and B. The assumption being made here is that each part A and B is a separate entity, when in fact it is all one shoelace. This simplifying assumption that makes it possible to do the algorithm, and fortunately does not alter the answer substantially. Now, we begin to tie the shoe by putting A over B, represented as a "division":
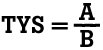 At this stage, we have a new A and a new B, both slightly shorter than they were originally, since some of each is "used up" in the knot. The question is: can we simplify the problem by still calling the laces A and B, as there is not very much of the original A and B used up in the knot? If we can't accept this assumption, the algorithm becomes substantially more complicated and perhaps less useful (but more accurate). Even if we don't accept this assumption, there is going to be some error introduced in the form of round-off error, the error that occurrs "naturally" as a function of the amount of precision you have in your measuring tool and/or in your computational environment. This example is contrived and trivial, the the point is this: all along the way in attacking a problem computationally, you are confronted with the depth and breadth of the assumptions and simplifications that you will accept, and the error introduced through natural or computationally-induced artifacts. In this case, we can say that the error introduced by ignoring lace length in the knot itself is trivial, so we'll continue to call each lace by its original name, A and B. What is the next part of the algorithm? At this stage, we fold A and B each in half (mathematically multiply them by 0.5), then put the half-folded A over top (division) of the half-folded B. Once this operation is done, the algorithm is complete, and the entire algorithm TYS is as follows:
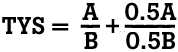 Once we have created an algorithm, we can use a wide variety of computational tools (including a pencil!) to generate a solution to the algorithm for a variety of conditions. This mathematical model of tying your shoe allows us to do simulations -- perform "what-if" scenarios by altering the input parameters or initial conditions of the physical event. I will be the first to admit that this is a "stretch", but I think it does make the following points, just to list a few:
|
in cooperation with the
National Center for Supercomputing Applications
© Copyright 1999-2000 The Shodor Education Foundation, Inc.