Quick Guide to DISCO Output

Quick Guide to DISCO Output

Output files will vary according to the molecule you are working with and the initial data you enter. However, the following example is a good demonstration of an average output file.

******************************************************* ******************************************************* **|||||||||||||||||||||||||||||||||||||||||||||||||||** **|||||||||||||||||||||||||||||||||||||||||||||||||||** **||||||| |||| ||||| ||||| ||||||| |||||||||** **||||||| || |||| |||||||| |||||||| | |||||||** **||||||| | | |||| |||||||||| |||| ||| ||||||** **||||||| || |||| |||||||||||| ||| ||||||** **||||||| ||| ||||| ||||| |||| ||| ||||||** **|||||||||||||||||||||||||||||||||||||||||||||||||||** **|||||||||||||||||||||||||||||||||||||||||||||||||||** **||||||||||||||||| ||||||||||||||||** **|||||||||||||||||||||||||||||||||||||||||||||||||||** **|||||||||||||||||||||||||||||||||||||||||||||||||||** **||||||| |||| |||| ||| |||| |||||||** **||||||| || |||| |||| ||||| |||||| ||| ||||||** **||||||| || |||| ||||| ||| |||||| ||| ||||||** **||||||| || |||| ||||||| || |||||| ||| ||||||** **||||||| |||| ||| |||| |||| |||||||** **|||||||||||||||||||||||||||||||||||||||||||||||||||** **|||||||||||||||||||||||||||||||||||||||||||||||||||** **THIS IS THE NCSA VERSION OF THE DISCO PROGRAM BASED** ** ON THE DISCO PROGRAM FROM THE ** ** UNIVERSITY OF MINNESOTA CRAY-2 CFT77 VERSION 1.50 ** ** ** ** THE NCSA VERSION MAY DIFFER SIGNIFICANTLY FROM THE** ** MINNESOTA PROGRAM ** ******************************************************* ** UNIVERSITY OF MINNESOTA CRAY-2 CFT77 VERSION 1.50 ** ******************************************************* ** DISCO IS AN EXPERIMENTAL CODE FOR DIRECT SCF AND ** ** MP2 CALCULATIONS, USING METHODS DESCRIBED IN: ** ** 1) J.ALMLOF, K.FAEGRI,JR., K.KORSELL, ** ** J.COMPUT.CHEM 3, (1982) 385. ** ** 2) S.SAEB0 & J.ALMLOF, CHEM.PHYS.LETT. 154 (1987) ** ** 521. ** ** THE AUTHORS ACCEPT NO RESPONSIBILITY FOR THE PER- ** ** FORMANCE OF OR RESULTS OBTAINED FROM THIS PROGRAM.** ** THIS PROGRAM, OR ANY PART THEREOF, MAY NOT BE: ** ** 1) REPRODUCED FOR FURTHER DISTRIBUTION. ** ** 2) INCORPORATED INTO ANOTHER PROGRAM. ** ** IF RESULTS OBTAINED FROM THIS PROGRAM ARE ** ** PUBLISHED, AN APPROPRIATE CITATION WOULD BE: ** ** J.ALMLOF, K.FAEGRI,JR., M. FEYEREISEN, & K.KORSELL** ** DISCO , A DIRECT SCF AND MP2 CODE. ** ** THE NCSA VERSION COURTESY OF HARRELL SELLERS ** ** ** ** ** ** Publications having results obtained with the ** ** ** ** N C S A - D I S C O ** ** ** ** program should acknowledge that NCSA-DISCO is ** ** courtesy of Harrell Sellers. ** ** ** ******************************************************* *******************************************************	DISCO Information This section provides copyright, publication, and reference information.
************** RUN OPTIONS ************************** FORTRAN JACOBI USED FOR DIAGONALIZE. STARTING OPTION PARAMETER IXXSTA : 2 INTEGRAL TEST TYPE : 2 MAXIMUM NUMBER OF S C F ITERATIONS : 50 BASIS SETS NOT ORTHOGONALIZED . INTEGRAL ELIMINATION CRITERION : 0.10E-09 S.C.F. GRAD. CONVERGENCE CRIT: 0.10E-01 BFGS UPDATE GRAD. CONVERGENCE CRIT: 0.10E-03 SYMMETRY BLOCKING IS USED IN SCF . INTEGRALS WILL BE STORED IN CORE . NEW SUPER ATOM NRCMAX AND NUCMAX : 0 0 AUFBAU FILLING WILL BE USED . *****************************************************	Run Options The run options are based on SCF Iterations. SCF, Self-Consistent Field Method, is a way of calculating atomic and molecular structures. The procedure begins with a set of approximate orbitals (a basis set) for all of the electrons in the system. One electron is selected, and the potential in which it moves is calculated by "freezing" the distribution of all the other electrons and treating their averaged distribution as a single ("centrosymmetric") source of potential. The Schroedinger equation is then solved for the selected electron, and a new, more accurate orbital is calculated for that electron. The procedure is then repeated for all the other electrons in the system. Once each electron has been evaluated, we are at the end of one cycle. The process begins again with the first electron evaluated, using the newly calculated orbitals as the starting point. This process continues through the iteration process until a pass through the calculations does not change the values of the orbitals. We can then say that the orbitals are "self-consistent". When we apply the SCF method to molecules, we are actually looking at linear combinations of atomic orbitals (LCAO); the SCF calculations are applied to these orbitals, not to the atomic orbitals. Note also that the basic SCF method neglects the effect of each electron on the current "target" electron; the only thing the target electron sees is the average of the other electrons. In other words, there is no correlation with the other electrons. This is a fairly major approximation. Newer SCF algorithms look to take into account the individual effects of the other electrons in the system. In this example, the DISCO runs a maximum of 50 iterations. This means that even if the molecule hasn't proven itself self-consistent after 50 runs, the programs terminates.
THE POINT GROUP OF THE MOLECULE IS ...CN THE ORDER OF THE PRINCIPAL AXIS IS ... 1 IRREDUCIBLE REPRESENTATIONS AG AU	Symmetry The symmetry of a molecule is one important method for classification. Knowing the symmetry gives you a great deal of information about that molecule. Symmetry is classified in several ways. An action that leaves an object looking the same after it has been carried out is called a symmetry operation. There are five kinds of symmetry operations: Identity, n-fold rotation, Reflection in a mirror plane, Inversion through a centre of symmetry, and n-fold improper rotation. The explanations of each is listed in the table below. Identity Consists of doing nothing; the corresponding symmetry element is the entire object n-fold rotation A rotation about an n-fold axis of symmetry, Cn (the corresponding element), is a rotation through 360 degrees/n Reflection in a mirror plane If the reflected plane is parallel to the principal axis, it is called 'vertical', if it is perpendicular to the principal axis, it is 'horizontal'. Inversion through a centre of symmetry The ability to take each point in a molecule, move it to the centre of the molecule, and then move it out the same distance on the other side and end up with the molecule looking the same. n-fold improper rotation A composition of two transformations. The first is a rotation through 360 degrees/n and the second is a reflection through a plane perpendicular to the axis of that rotation. Another classification is the Mulliken Symmetry Symbols and is listed in the table below. Meaning A Symmetrical with respect to a 360/n degree rotation about the n-fold principal axis B Antisymmetrical with respect to a 360/n degree rotation about the n-fold principal axis E Doubly degenerate T Triply degenerate Subscripts 1 Symmetrical with respect to a 180-degree rotation about a C-2 axis perpendicular to the principal axis, or with respect to reflection in a sigma-v plane if there are no such C-2 axes 2 Antisymmetrical with respect to a 180-degree rotation about a C-2 axis perpendicular to the principal axis, or with respect to reflection in a sigma-v plane if there are no such C-2 axes g Symmetrical with respect to inversion u Antisymmetrical with respect to inversion Superscripts ' Symmetrical with respect to reflection in a sigma-v plane " Antisymmetrical with respect to reflection in a sigma-v plane Molecules with like symmetries have similar properties. For example, polarity is a property that can be determined immediatly upon knowing the point group symmetry. Polarity is a charge distribution which creates a dipole moment perpendicular to the symmetry axis. Chirality is another property that can be determined by symmetry. Chiral molecules rotate the plane of polarized light. The H2 molecule in this example is reported to be CN with N = 1 or C1. This means it follows the Identity symmetry operation. No matter which way you rotate it, it always looks the same.
--------------------BASIS SET FOR H321G -------------------- S EXPONENT COEFFICIENTS 5.447178 0.1562850 0.0000000 0.824547 0.9046910 0.0000000 0.183192 0.0000000 1.0000000 --------------------BASIS SET FOR H321G -------------------- S EXPONENT COEFFICIENTS 5.447178 0.1562850 0.0000000 0.824547 0.9046910 0.0000000 0.183192 0.0000000 1.0000000	Basis Set Information As you may recall from previous readings, a basis set is a table of numbers which mathematically estimate where the electrons can be found. The general expression for a basis function is Basis Function = N * e(-alpha * r) Where: N = Normalization constant alpha = Orbital exponent r = Radius in angstroms In this example, we utilized a 321G basis set. This means we have three sets of constants for each atom. Notice in this case, the basis information for each atom is the same. This is because both atoms are the same. In the case of a 321G, you are adding three basis sets in order to calculate the molecular orbital. However, you must use a contraction coefficient when adding these three values. Each basis set has its own contraction coefficient. The molecular orbital equation is shown below. MO = d*BF1 + d*BF2 + d*BF3 Where: d = Contraction Coefficient BFn = Basis Function The first column of figures is the alpha values or orbital exponents, the second is the contraction coefficient and the third is the contribution factor by p orbitals (you do not need to worry about the third column). You can check these values by using the Gaussian Basis Set Order Form. However, the Hydrogen atom has already been calculated for you as an Example. If you feel that you need further review of basis sets, look at the Basis Sets reading.
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * ATOM ATOMIC COORDINATES NUMBER OF CHARGE X Y Z SHELLS * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * H321G H 1.0 0.0000000 0.0000000 1.0000000 2S H321G H 1.0 0.0000000 0.0000000 0.0000000 2S	Cartesian Coordinates (Standard Orientation) This section feeds back information you entered into the original form. The first column tells you the basis set you are using for each atom. In this case, we are using the 321G for both hydrogen atoms. The next column tells you which atom the following data is for. The third column gives the atomic charge. The following three columns are the x, y, and z coordinates that you entered before the run. The last column displays the number of shells. In this case each hydrogen has one electron which it shares with the other. Thus, there are two electrons in the molecule, each filling 1 s-shell. Hence, each atom now has 2s shells filled.
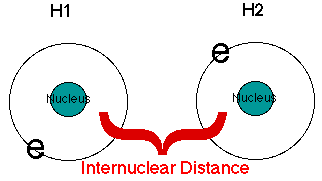
INTERNUCLEAR DISTANCES (ATOMIC UNITS) ANGSTROMS ********************************************************** * H 1 <---> H 2 ( 1.889727) 1.000000 * **********************************************************	Internuclear Distances This section gives the internuclear distances between atoms. Remember that the internuclear distance is the distance between the nuclei of two atoms. In this case, one hydrogen atom has been labeled H1 and the other H2. The two headed arrow represents the bond between the two atoms. The distances follow. Notice that the distances are given in Atomic Units and in Angstroms. In previous sections we told you: 1 bohr = 1 atomic unit = 0.527977 angstroms Does this conversion work with the data given in this output?
INPUT UNIT OF LENGTH = ANGS TOTAL NUMBER OF SHELLS = 4 TOTAL NUMBER OF BASIS FUNCTIONS = 4 NUMBER OF ELECTRONS = 2 CHARGE OF MOLECULE = 0 STATE MULTIPLICITY = 1 NUMBER OF OCCUPIED ORBITALS = 1 TOTAL NUMBER OF ATOMS = 2 NUMBER OF SUBGROUPS = 1	Fundamental Molecule Descriptors This section provides basic information about the molecule. Notice that the total number of shells is equal to the total number of basis functions. There is a total of two electrons (one from each hydrogen atom). The total charge on the molecule is zero because you have one hydrogen with a positive charge and another with a negative charge so that the two charges cancel out each other. The State Multiplicity, also known as the Spin Multiplicity, takes a little calculating. The equation used to calculate this number is: State Multiplicity = 2*s + 1 Where: s = Number of unpaired electrons In this case, both electrons are paired in the same orbital. 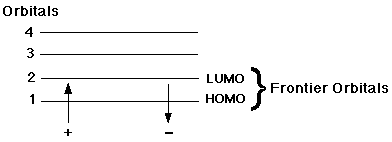Thus, there are no unpaired orbitals and our equation is 2*0 + 1 = 1 . This diagram above also explains why only one of the four orbitals is occupied. The total number of atoms we have already determined to be two. You do not need to know subgroups yet.
ONENEW| TIME IN ONENEW : 0.00 VTEST| ****** VECTOR ANALYSIS ************************ VTEST| * ERROR OF SYMMETRY ORTHOGONALITY : 0.00E+00 * VTEST| * ERROR OF OVERLAP ORTHOGONALITY : 0.44E-15 * VTEST| *********************************************** **** SCF INFORMATION **** REPRESENTATION NUMBER : 1 REPRESENTATION SYMBOL : AG NUMBER OF ORBITALS : 4 MAIN| MAXIMUM AREA NEEDED FOR MATRICES : 81 MAIN| MAXIMUM AREA NEEDED FOR INTEGRALS : 51043 MAIN| MAXIMUM AREA NEEDED FOR CALCULATION: 51124 MAIN| MAXIMUM AREA AVAILABLE IN AREAL : 16000001	???
AUFBAU TOTAL: 1 --------------------SCF ITERATION: 2 -------------------------------------- TOTAL CORE : 51220 TOTAL ENERGY : -0.48842563 NUCLEAR ENERGY : 0.52917710 ONE-ELEC. ENERGY : -0.92979348 DIPOLE : 0.00000000 OPEN-SHELL ENERGY: 0.00000000 DIPOLE : 0.00000000 TWO-ELEC. ENERGY : -0.08780925 DIPOLE : 0.00000000 NORM OF GRADIENT : 0.2127E+01 AUFBAU TOTAL: 1 TWOEL TIME USED : 0.00 SEC. S C F TIME USED : 0.00 SEC. --------------------SCF ITERATION: 3 -------------------------------------- TOTAL ENERGY : -1.07681931 NUCLEAR ENERGY : 0.52917710 ONE-ELEC. ENERGY : -1.11041647 DIPOLE : 0.00000000 OPEN-SHELL ENERGY: 0.00000000 DIPOLE : 0.00000000 TWO-ELEC. ENERGY : -0.49557994 DIPOLE : 0.00000000 NORM OF GRADIENT : 0.1974E+00 GRADIENT RATIO : 0.9281E-01 AUFBAU TOTAL: 1 TWOEL TIME USED : 0.01 SEC. S C F TIME USED : 0.01 SEC. --------------------SCF ITERATION: 4 -------------------------------------- TOTAL ENERGY : -1.08695786 NUCLEAR ENERGY : 0.52917710 ONE-ELEC. ENERGY : -1.10630902 DIPOLE : 0.00000000 OPEN-SHELL ENERGY: 0.00000000 DIPOLE : 0.00000000 TWO-ELEC. ENERGY : -0.50982594 DIPOLE : 0.00000000 NORM OF GRADIENT : 0.1091E+00 GRADIENT RATIO : 0.5530E+00 AUFBAU TOTAL: 1 TWOEL TIME USED : 0.00 SEC. S C F TIME USED : 0.00 SEC. --------------------SCF ITERATION: 5 -------------------------------------- TOTAL ENERGY : -1.08998195 NUCLEAR ENERGY : 0.52917710 ONE-ELEC. ENERGY : -1.10300638 DIPOLE : 0.00000000 OPEN-SHELL ENERGY: 0.00000000 DIPOLE : 0.00000000 TWO-ELEC. ENERGY : -0.51615267 DIPOLE : 0.00000000 NORM OF GRADIENT : 0.6152E-01 GRADIENT RATIO : 0.5636E+00 AUFBAU TOTAL: 1 TWOEL TIME USED : 0.01 SEC. S C F TIME USED : 0.01 SEC. --------------------SCF ITERATION: 6 -------------------------------------- TOTAL ENERGY : -1.09093092 NUCLEAR ENERGY : 0.52917710 ONE-ELEC. ENERGY : -1.10084476 DIPOLE : 0.00000000 OPEN-SHELL ENERGY: 0.00000000 DIPOLE : 0.00000000 TWO-ELEC. ENERGY : -0.51926327 DIPOLE : 0.00000000 NORM OF GRADIENT : 0.3503E-01 GRADIENT RATIO : 0.5695E+00 AUFBAU TOTAL: 1 TWOEL TIME USED : 0.00 SEC. S C F TIME USED : 0.00 SEC. --------------------SCF ITERATION: 7 -------------------------------------- TOTAL ENERGY : -1.09123685 NUCLEAR ENERGY : 0.52917710 ONE-ELEC. ENERGY : -1.09952003 DIPOLE : 0.00000000 OPEN-SHELL ENERGY: 0.00000000 DIPOLE : 0.00000000 TWO-ELEC. ENERGY : -0.52089392 DIPOLE : 0.00000000 NORM OF GRADIENT : 0.2006E-01 GRADIENT RATIO : 0.5726E+00 AUFBAU TOTAL: 1 TWOEL TIME USED : 0.01 SEC. S C F TIME USED : 0.01 SEC. --------------------SCF ITERATION: 8 -------------------------------------- TOTAL ENERGY : -1.09133685 NUCLEAR ENERGY : 0.52917710 ONE-ELEC. ENERGY : -1.09873115 DIPOLE : 0.00000000 OPEN-SHELL ENERGY: 0.00000000 DIPOLE : 0.00000000 TWO-ELEC. ENERGY : -0.52178281 DIPOLE : 0.00000000 NORM OF GRADIENT : 0.1152E-01 GRADIENT RATIO : 0.5742E+00	SCF Iterations: Each time an iteration is performed, the energy of the molecule changes. The data from this output file is compiled in the table below. The first column lists each iteration; the second, the calculated energy level; the third, the difference in energy between successive iterations. 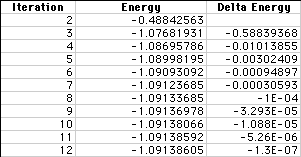In the graph below, we have shown the energy for each iteration. Notice how the energy converges to a minimum as highlighted by the arrows. 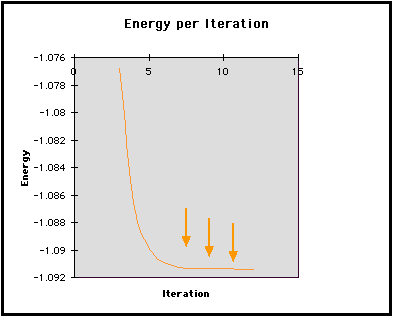To converge is defined by Webster's Dictionary as: 1) to tend or move toward one point or one another 2) to come together and unite in a common interest or focus 3) to approach a limit as the number of terms increases without limit This second graph shows the difference in Energy between iterations. Initially, calculated values differ greatly from one iteration to the next. This graph displays the large gap between these initial values. It also shows the difference approaching zero as the energy of the molecule converges to its minimum.
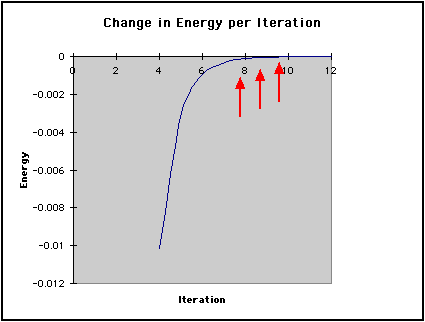***** FINAL SCF - RESULTS AFTER 12 ITERATIONS. ***** TOTAL ENERGY : -0.109138604817679D+01 ONE-ELEC. ENERGY : -0.219525790814399D+01 TWO-ELEC. ENERGY : 0.574694759967201D+00 NUCLEAR ENERGY : 0.529177100000000D+00	Final Energies Koupmans' Theorem The total energy is the sum of the energies in the orbitals and the energy in the nucleus. The one-electron energy is the ionization energy. Ionization energy can be defined by Koupmans' Theorem. Koupmans' Theorem states that the ionization energy of an atom or molecule equals the energy of the orbital from which the electron is removed.
EIGENVECTORS AND ORBITAL ENERGY .....................................AG ..................................... #/OCC. 1/ 2.00 2/ 0.00 3/ 0.00 ENERG. -0.5229 0.1881 1.0676 H S 0.25171 -0.14932 -0.88331 H S 0.36885 -1.17827 0.67240 H S 0.25171 0.14932 -0.88331 H S 0.36885 1.17827 0.67240 ****************************************************************************** *******************************ORBITAL ENERGIES******************************* ****************************************************************************** 1 AG -0.5229 AU -14.2299 EV 2.00 2 AG 0.1881 AU 5.1183 EV 0.00 3 AG 1.0676 AU 29.0519 EV 0.00 4 AG 1.2987 AU 35.3398 EV 0.00 ******************************************************************************	Orbital Energies LUMO/HOMO This section is divided into two. The top part shows the distribution of charges. Each hydrogen atom occupies both s-orbitals. That is why there are four rows of hydrogens. The three columns represent the first three orbitals. The fourth orbital is not shown in this output file. Notice that the first orbital is occupied by the two electrons and that the second and third orbitals are empty. This makes the first orbital the HOMO (Highest Occupied Molecular Orbital) and the second orbital the LUMO (Lowest Unoccupied Molecular Orbital). The HOMO and LUMO are also known as the Frontier orbitals. The bottom section lists each orbital in rows and gives the charge on that orbital in Atomic Units or Hartrees and in Electron Volts (the more common measurement. The conversions factor is 27.21EV = 1AU. Check to see if this conversion works for this data. The fourth row in this section gives the number of electrons present in each orbital. Can you identify the HOMO and LUMO?
GROSS CHARGE OF BASIS FUNCTIONS ATOM H 1 : S : S : : 0.342 : 0.658 : ATOM H 2 : S : S : : 0.342 : 0.658 : GROSS CHARGE OF SHELLS. ATOM H 1 : S : S : : 0.342 : 0.658 : ATOM H 2 : S : S : : 0.342 : 0.658 : GROSS ATOMIC CHARGE AND OVERLAPS. H 1 H 2 H 1 1.000 H 2 0.361 1.000 ******************************************************************************	Atomic Charges This section is another display of the distribution of charges. Notice that most of the charges add to 1.000, thus showing the full 100% charge of each electron.
MOPLT3D|****************************************** MOPLT3D|********* 3D MO PLOTTING ROUTINE ********* MOPLT3D|****************************************** ***VISUALIZATION VOLUME*** XNUM: 31 YNUM: 31 ZNUM: 31 XMAX: 9.4486 YMAX: 9.4486 ZMAX: 9.4486 XMIN: -9.4486 YMIN: -9.4486 ZINN: -9.4486 TIME: 0.7500	Plotting Parameters This is a list of the parameters used in the visual display of the molecule. It is determined by the program and not changeable by users.
TIME IS DISCO : 0.84 SEC. Disco Done	CPU Time The CPU time is the amount of time it takes to complete the run. This is different than the Wall time which is the time it takes to get an answer back on your machine. The way DISCO works is the data that you enter into the interface is packaged up and sent to the main computer at NCSA. This main computer is being used by multiple scientists. Your job is put in line with the rest of the jobs that other people have sent. The time it takes your job to run on the NCSA computer is the CPU time. The time it takes to send your job, wait in line, run on the NCSA computer, and receive the results on your computer is the Wall time. Depending on how busy the NCSA computer is will determine the discrepency between the two times.