ChemVizOverview |
Eigenfunctions and Eigenvalues |
| Eigenfunctions and Eigenvalues Overview Materials
Readings Lab Activities Support Materials Related Links Developers' Tools
|
Eigenfunctions and eigenvalues are quite important mathematical concepts in
science. Perhaps no where is this more true than with quantum mechanics.
Indeed, the primary equation of quantum chemistry -- Schrödinger's
equation -- is itself an eigenfunction.
H
where A good example of eigenvalues and eigenfunctions comes from calculus (if you haven't had calculus, you should still be able to understand this example!). Take the function: f(x) = x^2 (x squared) In calculus, there is an operation called differentiation. Remember, an operation is just a mathematical change that you do -- addition, multiplication, substraction, and division are all operations (the most basic ones). Differentiation is a process that manipulates or changes a function for some (hopefully) useful purpose. In this case if I do a differentiation operation on the function f(x), this would be the result: Differentiate [ f(x)] = 2x Notice that I now have a different function -- f(x) = 2x -- than I started with. Since I end up with a different function than the one I started with, I DO NOT have an eigenfunction. Let's look at another function: f(x) = exp(2x) [the exponential of 2 times x] Now, if I again use the same operation -- differentiation -- on this function, I will get this new function: Differentiate [f(x)] = 2 exp(2x) Notice that the original function -- exp(2x) -- is still there, but now multiplied by 2. Because this operation gives me an answer with the original function still intact, it is called an eigenfunction. The value of 2 that (in this case) is multiplied times that function is called the eigenvalue. Now look at Schrödinger's equation again. The operation is the process described by the Hamiltonian, which you should recall from the first session. The first value of psi (which is operated on by the hamiltonian) is the original function of interest. When we, with the help of a computational approach, operate on psi with the hamiltonian, we get back an eigenvalue of E, the energy of the system, and the original function psi.
|
in cooperation with the
National Center for Supercomputing Applications
© Copyright 1999-2000 The Shodor Education Foundation, Inc.
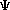 = E
= E