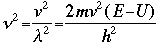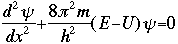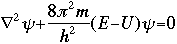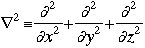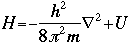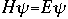ChemVizOverview |
Overview of Schroëdinger's Equation |
| Schroëdinger's Equation Overview Materials
Readings Lab Activities Support Materials Related Links Developers' Tools
|
How Much Do I Already Know?Key Points
OverviewSchroëdinger's Equation: A Historical PerspectiveAtomic structure is something that is of much interest to chemists and physicists, as it is difficult to theoretically explain observable phenomenon without a sense of the nature of the atom and its behavior. You might remember from the reading on basic quantum chemistry that Niels Bohr developed a model of the atom that resembled a planetary system, with the "sun" (nucleus) in the middle with the "planets" (electrons) circling around outside in "orbits". Electrons are viewed as being "little spherical balls" that behave according to classical Newtonian physics. It was soon determined, however, that this model was too simplistic and that it often did not fit observed phenomenon. More and more rules and exceptions to the rule were required to make the data fit. Not good science.Then in 1910, Louis DeBroglie, became interested in two of Einstein's major pieces of research: the theory of relativity and the photoelectric effect. DeBroglie thought that relativity might shed some light on Einstein's work with the photoelectric effect. DeBroglie was interested in the idea that light can be described as many "particles" of electrons, as well as being "waves," much like the waves seen in a pond when you throw in a stone or the waves created by plucking a stringed instrument. DeBroglie, in his search for a description of the wave behavior, was not taken too seriously, at least until he was able to predict what the expected wavelengths might be. DeBroglie, in his efforts to attract believers to the cause, was fortunate in that Einstein caught wind of his ideas and told his friend Max Born, who initiated a series of experimental activities which supported the concept of electron waves. A physicist by the name of Erwin Schroëdinger read some of Einstein's comments on DeBroglie, and decided that this might not be a bad thing to investigate. In classical physics, there is a series of equations that can be used to describe a wide variety of wave forms. The classical equation looks like this:
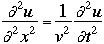 where
v the velocity of propagation t is the time
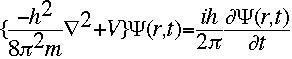 The symbol psi is a mathematical function that calculates the strength of the deBroglie wave at various positions in space. The rest of the components are as follows:
m = the mass of the particle  = a partial differential operator called the Laplacian operator = a partial differential operator called the Laplacian operatorV=the potential energy 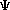 =psi, the wave function =psi, the wave functioni =the square root of -1 E = total energy of the system
The whole problem with all of this is that Schroëdinger's equation does not make it any easier to "visualize" what these waves looked like. They are not "real waves", like water waves, but rather mathematical waves described by a mathematical function. [It is interesting to note, that the Schroëdinger equation is not a "derivable" equation, meaning one that is built by using other simpler mathematical equations or postulates. It is, rather, what is known as an "inspired" equation.] So what did this equation do for knowing more about atomic structure? Bohr's orbital theory had the problem that if we wanted to describe the movement of an electron from Orbit 1 to Orbit 2, the rules more or less stated that the electron made an instantaneous leap from one level to the next. Schroëdinger's equation eliminated this illogical quantum jump, replacing it with a transitional process in which the wave pattern gradually fades out, while the new wave pattern fades in, during which time light is being emitted. Schroëdinger's equation made it possible to resolve a variety of the inconsistencies that had been present in previous theories. There were, however, still some problems. Max Born, in his experimental work on electron and atomic collisions, could not completely buy into the wave theory. Born's contribution was to develop a new interpretation of Schroëdinger's wave function. Born received a Nobel Prize for the realization that while psi was not a physical reality, the square of of psi could be shown to be the probability of finding a particle (in our case, an electron) at a certain location around the nucleus.
CALCULATIONS OF INTERESTOne of the initial quantum calculations was Bohr's calculation of the radial distance of the atomic orbitals. He used classical physics, in this case angular momentum and centrifugal force, to find what we now call the Bohr radius (a0).Starting with the equation of wave motion in one dimension: We can use the Schroëdinger equation to predict and/or calculate the energy of atoms as electrons move around. Schroëdinger's equations can be solved exactly only for one-electron atoms. In order to describe the position of the electron relative to the nucleus, we can calculate how the wave function varies as a function of the radial distance from the nucleus. For the hydrogen atom, the 1s, 2s, and 2p wave functions are given by the equations below:
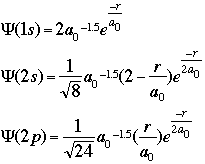 where:
r = the radial distance from the nucleus These equations only give us the probability of finding the electron on a single radial line, beginning at the nucleus and going to infinity. We are, however, more interested in locating the electron without regard to direction, not looking along a particular radial line but looking instead at the probability that the electron is in a very thin spherical shell at distance r. This probability is obtained by averaging the square of psi over all angles. This function is known as the radial probability function. A plot of P(r) for the 1s, 2s, and 2p wavefunctions looks like this:
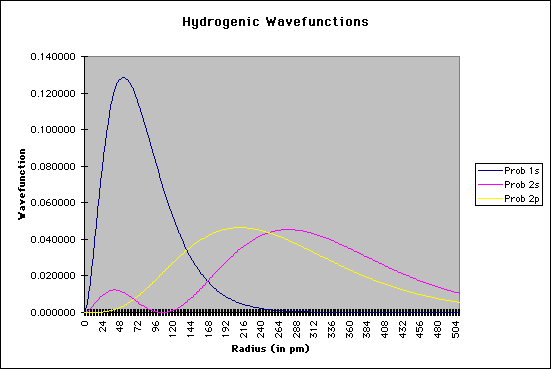
Solving Schroëdinger's Equation: Computational ChemistryWhat, you might ask, is the purpose of all of this, and how does it help the chemist? Schroëdinger's equation is one of the starting points for most of the quantum chemical calculations that are done now, mostly using supercomputer technology. It should again be emphasized that the equation cannont really be solved analytically for more than one particle; this means we can solve the equation for hydrogen, but not for helium or other elements or compounds. There have been, however, a number of mathematical methods that use approximation techniques to help chemists to get a sense of the atomic and/or molecular structure. Several of the methods are as follows:
As the table below shows, there are a number of approximations and other mathematical representations (including a concept known as basis sets, which will be explored in great detail!) that are used computationally. As the top part of the chart below shows, there are a number of techniques, such as the Hartree-Fock (HF) approximation, which are relatively simplistic. Moving from the left all the way to right, we have the correlation interaction (CI) method, which better approximates the "true" solution to Schroëdinger's equation, but is computationally more difficult and more "expensive". 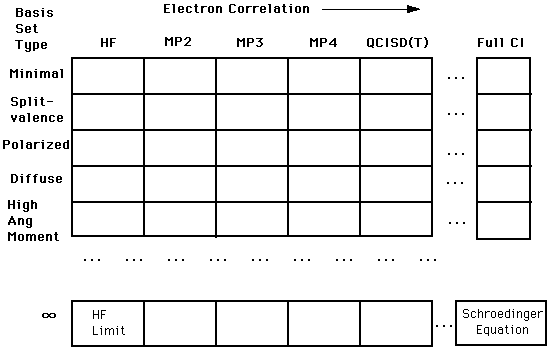
|
in cooperation with the
National Center for Supercomputing Applications
© Copyright 1999-2000 The Shodor Education Foundation, Inc.
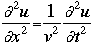
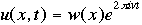
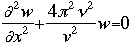
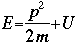
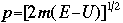
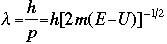
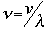 :
: