ChemViz

As a quick review, remember that scientists are mainly interested in the properties of molecules. One characteristic of a molecule that explains a great deal about these properties is their molecular orbitals. Recall the following diagram regarding what the scientist must know in order to calculate the molecular orbitals.

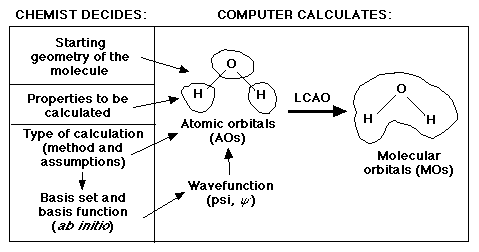One of the three major decisions for the scientist is which basis set to use. There are two general categories of basis sets:

Minimal basis sets: a basis set that describes only the most basic aspects of the orbitals
Extended basis sets: a basis set with a much more detailed description

Basis sets were first developed by J.C. Slater. Slater fit linear least-squares to data that could be easily calculated. The general expression for a basis function is given as:

Basis Function = N * e^{(-alpha * r)}

where:
N =	normalization constant
alpha =	orbital exponent
r =	radius in angstroms

This expression given as a Slater Type Orbital (STO) equation is:

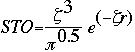
Now it is important to remember that STO is a very tedious calculation. S.F. Boys came up with an alternative when he developed the Gaussian Type Orbital (GTO) equation:

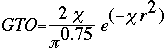
Notice that the difference between the STO and GTO is in the "r." The GTO squares the "r" so that the product of the gaussian "primitives" (original gaussian equations) is another gaussian. By doing this, we have an equation we can work with and so the equation is much easier. However, the price we pay is loss of accuracy. To compensate for this loss, we find that the more gaussian equations we combine, the more accurate our equation.

All basis set equations in the form STO-NG (where N represents the number of GTOs combined to approximate the STO) are considered to be "minimal" basis sets. (Remember our definition of minimal.) The "extended" basis sets, then, are the ones that consider the higher orbitals of the molecule and account for size and shape of molecular charge distributions.

There are several types of extended basis sets:

Double-Zeta, Triple-Zeta, Quadruple-Zeta

Split-Valence

Polarized Sets

Diffuse Sets

Double-Zeta, Triple-Zeta, Quadruple-Zeta

Previously with the minimal basis sets, we approximated all orbitals to be of the same shape. However, we know this is not true. The double-zeta basis set is important to us because it allows us to treat each orbital separately when we conduct the Hartree-Fock calculation. This gives us a more accurate representation of each orbital. In order to do this, each atomic orbital is expressed as the sum of two Slater-type orbitals (STOs). The two equations are the same except for the value of

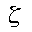(zeta). The zeta value accounts for how diffuse (large) the orbital is. The two STOs are then added in some proportion. The constant 'd' determines how much each STO will count towards the final orbital. Thus, the size of the atomic orbital can range anywhere between the value of either of the two STOs. For example, let's look at the following example of a 2s orbital:

In this case, each STO represents a different sized orbital because the zetas are different. The 'd' accounts for the percentage of the second STO to add in. The linear combination then gives us the atomic orbital. Since each of the two equations are the same, the symmetry remains constant.

The triple and quadruple-zeta basis sets work the same way, except use three and four Slater equations instead of two. The typical trade-off applies here as well, better accuracy...more time/work.

Split-Valence

Often it takes too much effort to calculate a double-zeta for every orbital. Instead, many scientists simplify matters by calculating a double-zeta only for the valence orbital. Since the inner-shell electrons aren't as vital to the calculation, they are described with a single Slater Orbital. This method is called a split-valence basis set. A few examples of common split-valence basis sets are 3-21G, 4-31G, and 6-31G.

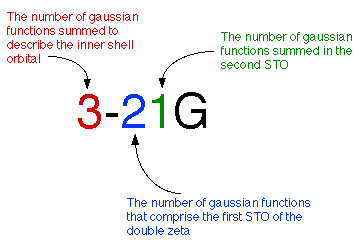
An example is given below. It is strongly encouraged that you take part of the class time to walk through this example with your class. It will be a tremendous help to the students understanding of this subject.

Here we are using a 3-21G basis set to calculate a carbon atom. This means we are summing 3 gaussians for the inner shell orbital, two gaussians for the first STO of the valence orbital and 1 gaussian for the second STO.
This is the output file from the gaussian Basis Set Order Form for carbon given a 3-21G basis set.

Here is another common method of displaying data. Notice the numbers are labeled so it is easy to match this data with the corresponding data in the output file.

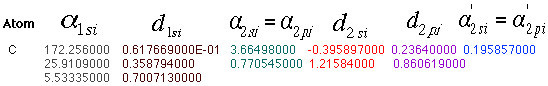
Once you have retrieved a basis set output file, you can use these numbers to calculate your equations. For a carbon, you will need three equations: 1s orbital, 2s orbital, and 2p orbital.

This equation combines the 3 GTO orbitals that define the 1s orbital.

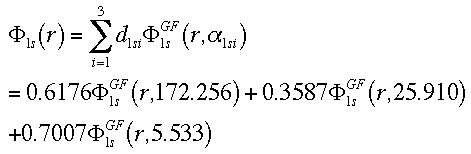
This equation combines the 2 GTO orbitals that make up the first STO of the double-zeta, plus the 1 GTO that represents the second STO for the 2s orbital.

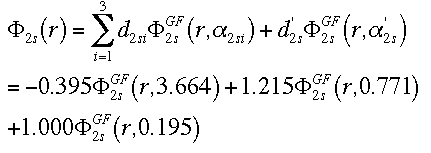
This equation combines the 2 GTO orbitals that make up the first STO of the double-zeta, plus 1 GTO that represents the second STO for the 2p orbital.

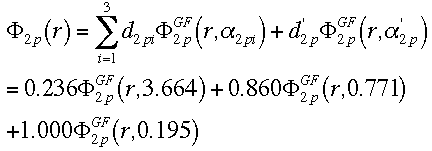
Now, using these three equations, we can calculate the LCAO for the carbon atom.

Polarized Sets

In the previous basis sets we have looked at, we treated atomic orbitals as existing only as 's', 'p', 'd', 'f' etc. Although those basis sets are good approximations, a better approximation is to acknowledge and account for the fact that sometimes orbitals share qualities of 's' and 'p' orbitals or 'p' and 'd', etc. and not necessarily have characteristics of only one or the other. As atoms are brought close together, their charge distribution causes a polarization effect (the positive charge is drawn to one side while the negative charge is drawn to the other) which distorts the shape of the atomic orbitals. In this case, 's' orbitals begin to have a little of the 'p' flavor and 'p' orbitals begin to have a little of the 'd' flavor. One asterisk (*) at the end of a basis set denotes that polarization has been taken into account in the 'p' orbitals. Notice in the graphics below the difference between the representation of the 'p' orbital for the 6-31G and the 6-31G* basis sets. The polarized basis set represents the orbital as more than just 'p', by adding a little 'd'.

Original 'p' orbital

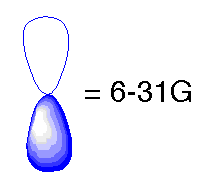
Modified 'p' orbital

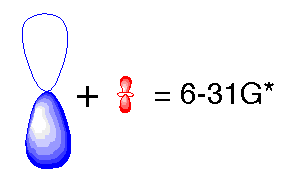
Two asterisks (**) means that polarization has taken into account the 's' orbitals in addition to the 'p' orbitals. Below is another illustration of the difference of the two methods.

Original 's' orbital

Modified 's' orbital

Diffuse Sets

In chemistry, we are mainly concerned with the valence electrons which interact with other molecules. However, many of the basis sets we have talked about previously concentrate on the main energy located in the inner shell electrons. This is the main area under the wave function curve. In the graphic below, this area is that to the left of the red dotted line. Normally the tail (the area to the right of the dotted line), is not really a factor in calculations.

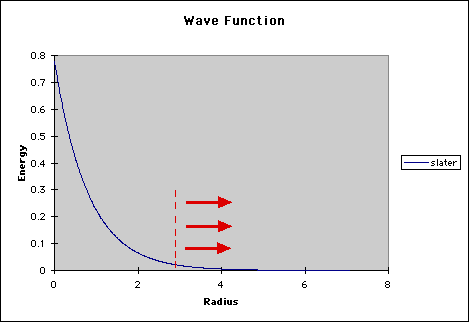
However, when an atom is in an anion or in an excited state, the loosely bond electrons, which are responsible for the energy in the tail of the wave function, become much more important. To compensate for this area, computational scientists use diffuse functions. These basis sets utilize very small exponents to clarify the properties of the tail. Diffuse basis sets are represented by the '+' signs. One '+' means that we are accounting for the 'p' orbitals, while '++' signals that we are looking at both 'p' and 's' orbitals, (much like the asterisks in the polarization basis sets).

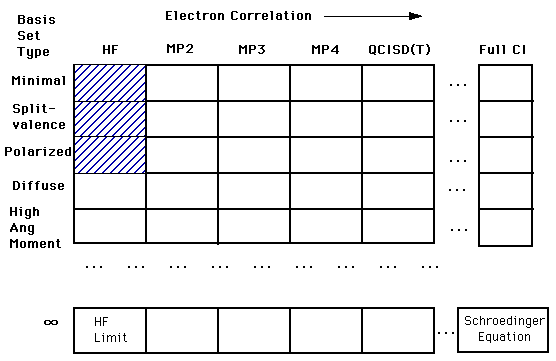
The tradeoff/relationship between basis sets and accuracy is represented in the diagram below. Our ultimate goal is to calculate an answer to the Schroëdinger's Equation (right bottom corner). However, we are still a long way from being able to complete this calculation. Right now we are in the top left corner of the chart. In that first box, we are treating each electron independently of the others. As you move across to the right, you find calculations that account for the interactions of electrons. As you move down the column you find more complex and more accurate basis set calculations. Students will only be expected to understand the shaded regions.

There are other trade-offs for using each type of basis set. The more complex basis sets are more accurate but, they use up a great deal of computing time. Whenever you run a computational chemistry calculation you will be using time on a computer. Normally, the computer that will be running the calculation will be one that is shared with many other people doing other calculations. Thus, it is important that you act responsibly when choosing which basis set to use. You should pick one that is efficient for your use. This means that you should consider how much time it will take to run the molecule and use the basis set that will run the fastest without compromising your desired level of accuracy.

Developed by

The Shodor Education Foundation, Inc.
in cooperation with the
National Center for Supercomputing Applications

ChemViz

Lab Activities

Background Reading for Basis Sets:

Students

Teachers

Basis Function = N * e(-alpha * r)

where:

N =

normalization constant

alpha =

orbital exponent

r =

radius in angstroms

Double-Zeta, Triple-Zeta, Quadruple-Zeta

Split-Valence

Polarized Sets

Original 'p' orbital

Modified 'p' orbital

Original 's' orbital

Modified 's' orbital

Diffuse Sets

Basis Function = N * e^{(-alpha * r)}