ChemViz

Lab Activities

Basis Sets, Functions, and CPU Time Lab Procedure:

Home

Basis Sets Lab Activity

Basis Set Main Page

Students

  • Introduction
  • Objectives
  • Background Reading
  • Procedure
  • Questions
  • Further Work
  • References/Support Materials

    Teachers

  • Additional Background
  • Materials
  • Standards
  • First year chemistry curriculum concepts
  • Second year chemistry curriculum concepts

    Readings

  • Overview
  • Atomic Orbitals

    Lab Activities

  • Z-matrices
  • Basis Sets
  • Geometry Optimizations
  • Ionization Energies

    Support Materials

  • Interactive Tools
  • Glossary of Terms
  • Quick Guide to DISCO Output File

    Related Links

  • ChemViz
  • Computational Chemistry
  • SUCCEED's Computational Chemistry

    Developers' Tools

  • What's New?
  • Discussion Board
  • Team Members
  • Email the Group

  • Contact Webmaster
    		•

    Procedure:

    Group Part:

  • In order to conduct this lab, you will need a spreadsheet and a Waltz Interface.
  • The molecules we are using in this lab are alkanes. They have the formula CnH2n+2. Alkanes are made up of n carbons linked together in a line with hydrogens jutting off every carbon. All of the bonds in alkanes are single bonds. The entire class will be collecting data to use for analysis. Split up the molecules so that each group will run a geometry optimization for two molecules. The more molecules the class runs, the better your results. When dividing up the molecules, skip every third alkane in the sequence. (ex. CH4, C2H6, C4H10)
  • You should set your spreadsheet up as follows:

  • You will use Waltz to run each molecule THREE times: once with an STO-3G, once with a 3-21G, and once with a 6-21G.
  • Once your run has completed, you will need to extract two pieces of information from the output file,
    1. The number of basis functions used.

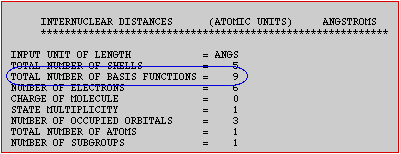
    2. The CPU time. (Remember that the CPU time is different from the Wall time. The CPU time is the time it took to complete the run on the computer. The Wall time is the time it took for you to get your answer back after you clicked the execute button.)

      Class Part:

    3. Once the class has collected all the data, compile it all into one spreadsheet.
    4. Graph the number of basis functions versus the number of carbons in each molecule. Do this for each of the 3-21G and 6-21G basis sets. You should have two graphs. What do you observe about the shape of each graph?
    5. Try to write two equations (one for each basis set) which give the number of basis functions (bf) for a certain number of carbons (c) plus a certain number of hydrogens (h). (Clue: Use systems of equations)

      y bf = (a*c) + (b*h)

      What are the coefficients (a) and (b) in this equation (both are integers)?
    6. Let's test your equation. Calculate the number of basis sets needed to calculate the following molecules.
    7. Now graph the CPU time, in seconds, versus the number of basis functions calculated. What relationship do you see? Describe what happens to the CPU time required as the molecule gets extremely large.
    8. Try to predict what the CPU time will be for the molecules which haven't been calculated yet. Each group should take one molecule that had been skipped earlier and one that is larger than any that have already been tried. How accurate do you think your predictions are? Do you think that the prediction for a molecule between two that we calculated is any more or less accurate than the prediction for a molecule not in between two that we calculated? If so, why? Discuss the difference between these predictions with your group. Record your predictions.
    9. Now, each group should run the calculations for their two molecules. Record the data and share the results with the class.

    • Developed by
    Shodor logoThe Shodor Education Foundation, Inc.
    in cooperation with the
    National Center for Supercomputing Applications

    © Copyright 1999-2000 The Shodor Education Foundation, Inc.