ChemVizLab Activities |
Background Reading for Basis Sets: | |||||||
| Basis Sets Lab Activity
Students
TeachersReadings Lab Activities Support Materials
Related Links Developers' Tools
|
Key PointsThe objective of computational chemistry is to be able to mathematically express the properties of molecules. One of the most important properties is that of the molecular orbitals. Scientist use something called a basis set to approximate these orbitals.
There are two general categories of basis sets:
In the most general sense, a basis set is a table of numbers which mathematically estimate where the electrons can be found. An American physicist named J. C. Slater developed algorithms by fitting linear least-squares to data which could easily be calculated. Suddenly, basis sets became much easier to express. Slater's equation is known as the Slater Type Orbital or (STO). The equation is given below. The general expression for a basis function is given as:
Basis Function = N * e(-alpha * r)
|
where: | |
N = | Normalization constant |
alpha = | Orbital exponent |
r = | Radius in angstroms |
This expression given as a Slater Type Orbital equation is:
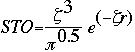
At this point, the STO equation looks like a great solution to finding the basis set of a molecule. Although the STO equation is a wonderful approximation for the molecular orbitals, the problem lies in the calculations. You see, calculating the STO of a molecule requires enormous amounts of work. This uses way too much time, even for super computers. Instead, a scientist by the name of S. F. Boys developed a method of using a combination of Gaussian Type Orbitals in order to express the STO equation. The following is the Gaussian Type Orbital (GTO) equation.
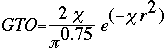
Notice that the difference between the STO and GTO is in the "r." The GTO squares the "r" so that the product of the gaussian "primitives" (original gaussian equations) is another gaussian. By doing this, we have an equation we can work with and so the equation is much easier. However, the price we pay is loss of accuracy. To compensate for this loss, we find that the more gaussian equations we combine, the more accurate our equation. In Basis Set Lab, you will be looking at a STO-3G basis set:
- The "STO" tells you that you are attempting to represent a STO equation for your molecule.
- The 3G tells you that in order to do this you are combining 3 gaussian primitives.
All basis set equations in the form STO-NG are considered to be "minimal" basis sets. (Remember our definition of minimal.) The "extended" basis sets, then, are the ones that consider the higher orbitals of the molecule.
The way to think about extended basis sets is to think of cleaning the kitchen floor. First you must sweep it to get all the big pieces of dirt. Then you go back and mop it to get the little bits of grime. Then you go over again and wax it to make sure everything is cleaned off and the floor is shiny. That is what you are doing to the molecules. Using the minimal basis set is like sweeping the floor. You are only describing the big properties. Using the extended basis sets is like mopping and waxing. You are fine tuning your description.
One way to mop up the little grime in your molecule descriptions is to use a method called "Split-Valence Basis Sets." The theory behind this method is that it would be extremely tedious to attempt calculating the expression for every single atomic orbital. Instead, by combining an expression for an orbital larger and smaller than the one we are looking at, we can approximate the orbital we are interested in. This method entails combining two or more STO's in order to describe an orbital. The STO's differ only by the value of their exponent (zeta) and can be manipulated by a constant "d" so that you can size the orbital to what you are looking for.
Now we need to wax the molecule. This is done by taking into account the Polarization effect. The polarization effect is the resulting effects when two atoms are brought close together. Taking into account the polarization effect means accounting for the d and f-shells by adding STOs of higher orbital angular momentum. The asterisk is the symbol used when taking into account polarization. One asterisk symbolizes accounting for the d-shell and two asterisks symbolizes the f-shell. If an asterisk is in parentheses symbolizes that polarization functions are added only to second-row elements. Standard polarization basis sets are 3-21G* and 6-31G*.
It is important that you understand how to read each basis set. For example, let us consider the 6-311G* basis set. The 6 represents the 6 gaussian primitives used to calculate the s-shell, the 3 represents the number of GTOs for one of the sp-shells and each 1 represents the number of GTOs for the other two sp-shells. The * represents the consideration of the d-shell. Other standard basis sets are STO-3G, 3-21G, 3-21G*, 4-31G, 6-31G, 6-31G*, 6-311G, and 6-311G*.
When dealing with anions, the use of diffuse functions is recommended. Indeed, this is the case when the electron density of a molecule is far removed from its nuclear center. Diffuse functions are also useful for systems in an excited state, for systems with low ionization potential, and systems with some significant negative charge attached. The presence of diffuse functions is symbolized by the addition of a plus sign, +, to the basis set designator: 6-31G+ or 6-31+G. Again, a second +, such as 6-31++G, implies diffuse functions added to hydrogens. The use of doubly-diffuse basis sets is especially useful if you are working with hydrides.
When choosing a basis set, choose the best basis set for your time limits. Remember, the better the basis set, the more time it will take to calculate!
Now, let's look at a typical basis set printout.
Here is a dump for H and C, showing data for the STO-2G basis set. You can see that for the hydrogen, 2 gaussian primitives are used to construct the s orbital. The first value of 1.309 is the orbital exponent, and the 0.430 is the contraction coefficient. With carbon, you see the addition value, so the first is the orbital exponent, the second is the s-part of the sp-hybrid, and the third part is the p-part of the sp-hybrid.
STO-2G
BASIS="STO-2G"
H 0
S 2 1.00
1.30975638 0.43012850
0.23313597 0.67891353
****
C 0
S 2 1.00
27.38503303 0.43012850
4.87452205 0.67891353
SP 2 1.00
1.13674819 0.04947177 0.51154071
0.28830936 0.96378241 0.61281990
***************Here is a dump of the 6-31G* for H and C. For H, there is only one valence electron, and it is represented by two orbitals, one constructed of 3 primitives and the other with 1 primitive. With C, the s-orbital is a core orbital, and is represented by 6 gaussian primitives. The sp-orbital, on the other hand, is a valence orbital, and is represented by two orbitals, one with 3 gaussians and the other with 1. Since this is a "*" , or polarized basis set, notice that there is some "d" character to the carbon atom.
6-31G*
BASIS="6-31G*"
H 0
S 3 1.00
18.73113700 0.03349460
2.82539370 0.23472695
0.64012170 0.81375733
S 1 1.00
0.16127780 1.00000000
****
C 0
S 6 1.00
3047.52490000 0.00183470
457.36951000 0.01403730
103.94869000 0.06884260
29.21015500 0.23218440
9.28666300 0.46794130
3.16392700 0.36231200
SP 3 1.00
7.86827240 -0.11933240 0.06899910
1.88128850 -0.16085420 0.31642400
0.54424930 1.14345640 0.74430830
SP 1 1.00
0.16871440 1.00000000 1.00000000
D 1 1.00
0.80000000 1.00000000
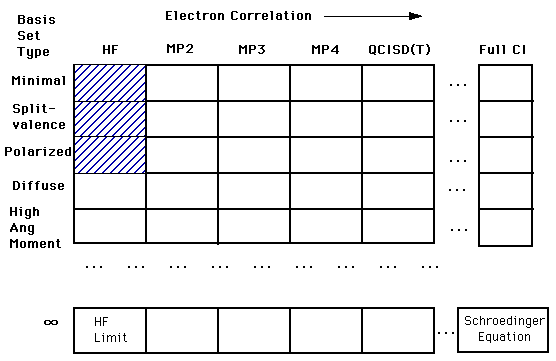
****The relationship between basis sets and accuracy is represented in the diagram below. Our ultimate goal is to calculate an answer to the Schroëdinger's Equation (right bottom corner). However, we are still a long way from being able to complete this calculation. Right now we are in the top left corner of the chart. In that first box, we are treating each electron independently of the others. As you move across to the right, you find calculations that account for the interactions of electrons. As you move down the column you find more complex and more accurate basis set calculations. You will only be expected to understand the shaded regions.
in cooperation with the
National Center for Supercomputing Applications
© Copyright 1999-2000 The Shodor Education Foundation, Inc.