ChemViz

The geometry of a molecule determines many of its physical and chemical properties. This is why it is very important that we understand the geometry of a molecule when running computations. In computational chemistry we are specifically concerned with optimizing:

bond angles (degrees)
bond distances (angstroms)
dihedral angles (degrees)

You will learn more how this works below in the reading.

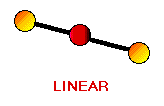
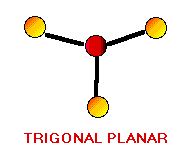
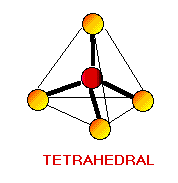
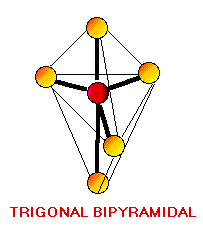
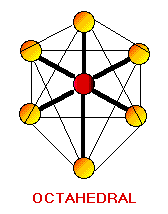
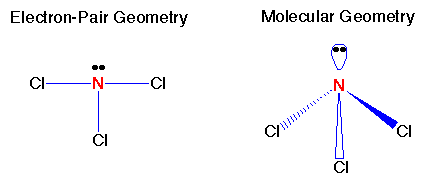
Remember the VSEPR (valence shell electron-pair repulsion) model. This model was designed by Ronald J. Gillespie. It states that the geometry of a molecule is determined by the repulsion forces of its valence electron pairs. At this time, it is important to remember that not all valence electrons are bonded. Electrons which are not bonded are called lone pairs. Lone pairs have the same effect as bonded electron pairs.

The repulsion forces of the valence electrons directly effect the size of the bond angle. The bond angle is the angle formed by two pairs of valence electrons and the central atom that connects the two. The stronger the repulsion strength, the larger the bond angle. The strength of repulsion goes in order:

lone pair - lone pair > lone pair - bond pair > bond pair - bond pair

Below are diagrams of various geometries as predicted by the VSEPR model.

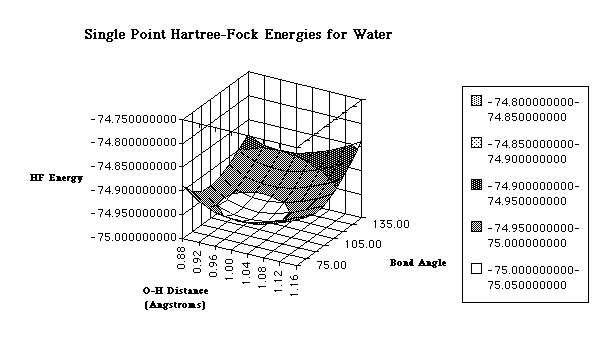
The lone pair electrons bring a twist to the idea of molecular geometry. Molecular geometry is the molecule's arrangement of atoms in space. It does not describe the placement of the electrons around each atom. To help with this, we have what is called the electron-pair geometry. The electron-pair geometry accounts for the location of all bond and lone pairs of electrons. Let's look at an example. Below is a Lewis structure of NCl₃. Here, the electron-pair geometry is tetrahedral while the molecular geometry is trigonal pyramidal. This is because the electron-pair geometry is concerned with the entire molecule and the molecular geometry is only concerned with the four atoms.

Although some textbooks choose to ignore the length of bonds in their geometry calculations, the bonds also have an effect on the geometry of the molecule. In fact, as you will soon see, their effect will be crucial in our computational geometry optimizations.

Now, up to this point, the determination of a molecule's geometry has been fairly simple: identify the valence electron pairs and determine the geometry. However, the VSEPR model is only a visual model and does not give us the detail needed in computational chemistry. For computational chemistry we need to be more precise by using cartesian coordinates, bond lengths and bond angles to find the optimal molecular geometry.

The arrangement of atoms in the molecules and more specifically the electrons around the atom determine the energy level of that molecule. In fact, the energy of a molecular system varies even with small changes in its structure. This is why geometry is so important when performing calculations. The objective of a geometry optimization is to find the point at which the energy is at a minimum because this is where the molecule is most stable and most likely to be found in nature.

One way to observe the effect of different geometries on energy level is to calculate a potential energy surface (PES). The potential energy surface is just a mathematical relationship correlating the particular molecular structure and its single point energy. They are usually represented by three-dimensional plots, although they can also be simple x-y plots for diatomic molecules.

Potential energy surfaces are characterized by distinct points:

Local Maxima - that point on the potential energy surface that is the highest value in a particular section or region of the PES
Global Maxima - that point on the potential energy surface that is the highest value in the entire PES
Local Minima - that point on the potential energy surface that is the lowest value in a particular section or region of the PES
Global Minima - that point on the PES that is the lowest value in the entire PES
Saddle point - a point on the PES that is a maximum in one direction and a minimum in the other. Saddle points represent a transition structure connecting two equilibrium structures.

and represents the equilibrium structure (optimal geometry) for the molecule. Different minima correspond to different conformations or structural isomers. They can also correspond to reactant and product structures in reaction systems. In addition, a PES can have a saddle point. This is a point that is a maximum in one direction and a minimum in the other. It takes its name in that graphically it looks like a saddle when plotted. A saddle point represents a transition structure connecting two equilibrium structures.

It is, therefore, the purpose of geometry optimizations to locate the minima based on some geometry for the molecule. Programs generally works to find a stationary point, a point on the potential energy surface where the forces are zero. They do this by first calculating the first derivative of the energy (also known as the gradient). At the minima, of the gradient the derivative of the energy with respect to its coordinates is zero, and has thus reached a stationary point. It should be noted that the gradient calculations don't always find the stationary point intended, and that some amount of experience, artistry, and luck are needed to coax the software to find the desired minimum!

In most programs that calculate geometry optimizations, the user specifies a beginning geometry (an educated guess), either as internal coordinates (Z-matrix), Cartesian coordinates, or in mixed format. Then a basis set is specified, the program will then compute the energy and the gradient at that point, decides if it has reached a stopping point (convergence), and then varies the geometry based on the size of the gradient. New integrals are calculated, new self-consistent field calculations are done, and a new energy and gradient are calculated. These steps are repeated until the program reaches convergence i.e. finds a stationary point.

There are a number of different algorithms for performing optimizations, such as Berny, Fletcher-Powell, quasi-Newton, and others. Most of these optimization algorithms also calculate the second derivative of the energy with respect to the coordinates, known as a Hessian. The Hessian serves to specify the curvature of the surface for that particular geometry, and thus "optimizes" the determination of how to vary the geometry for the next step. There are also things that the computational chemist can do to make optimizations behave better such as:

use of symmetry or dummy atoms
counting the number of internal coordinates
forcing strong coupling between internal coordinates
better initial guess for the geometry
providing an initial guess for the Hessian
testing stationary points

Developed by

The Shodor Education Foundation, Inc.
in cooperation with the
National Center for Supercomputing Applications