ChemViz

You have learned in earlier sessions that the geometry of a molecule determines many of its physical and chemical properties. This is why having accurate molecular geometries is so important to scientists. When calculating a molecular geometry, there are three measurements that we can make:

Bond angles (measured in degrees)
Bond distances (measured in angstroms)
Dihedral angles (measured in degrees)

The objective of geometry optimization is to find an atomic arrangement which makes the molecule most stable. Molecules are most stable when their energy is low. So, in order to optimize a molecular geometry, you want to test various possibilities to see which one has the lowest energy value. One way scientists do this is by creating a Potential Energy Surface (PES). A PES is a mathematical relationship between different molecular geometries and their corresponding single point energies. These values are usually displayed in a three-dimensional graph (although simple x-y plots are sometimes used for diatomic molecules). The three dimensions represent the bond angle, bond distance and the Hartree-Fock energy value. Below is an example of the PES of water.

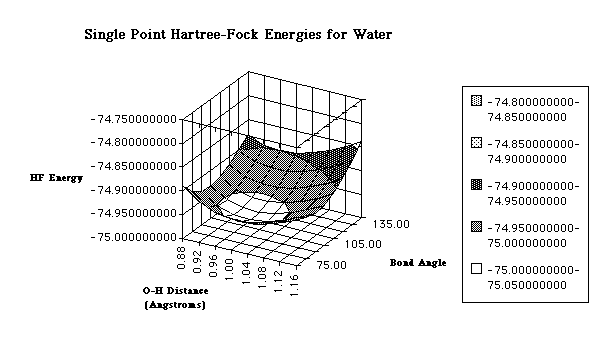Potential energy surfaces are characterized by distinct points:

Local Maximum - that point on the potential energy surface that is the highest value in a particular section or region of the PES
Global Maximum - that point on the potential energy surface that is the highest value in the entire PES
Local Minima - that point on the potential energy surface that is the lowest value in a particular section or region of the PES
Global Minima - that point on the PES that is the highest value in the entire PES
Saddle point - a point on the PES that is a maximum in one direction and a minimum in the other. Saddle points represent a transition structure connecting two equilibrium structures.

Below is a two dimensional graph so that you can clearly observe the various points. (A saddle point is not represented in this picture because it can only be shown in a three dimensional graph.)

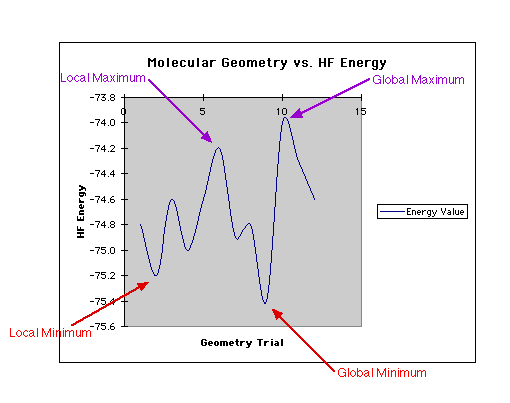Notice that a global minima represents the most optimal molecular geometry. The PES gives us a quick way to look and approximate a reasonable geometry.

To really understand the effect that geometry has on single point energy calculations, consider the example of n-butane below. In this example we compare literature values for single point energies with experimental values. More importantly, we compare single point energy calculations for various sized dihedrals. Notice how the energy values change as the dihedral grows.

Data Results:

CCCC Dihedral      Literature (Hehre's) Values     G94 (Gotwals') Values
     0                 -156.41638                      -156.42272
     30                -156.42670                      -156.42666
     60                -156.43106                      -156.43106
     90                -156.42958                      -156.42956
     120               -156.42673                      -156.42667
     150               -156.42963                      -156.42962
     180               -156.43247                      -156.43247

Graphical Results:

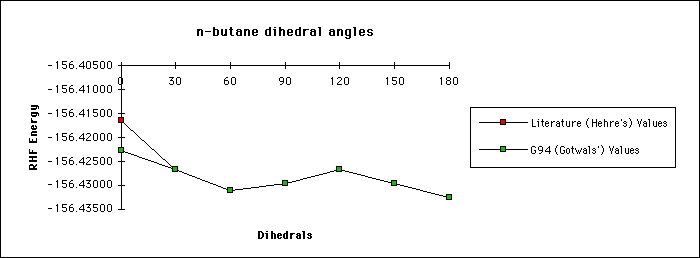
Most computational chemistry programs optimize molecular geometries for you. They do this by the series of steps that you read about in the Introduction. Remember that you typically must give the program an initial geometry and a basis set. From there the program calculates optimal values.

Developed by

The Shodor Education Foundation, Inc.
in cooperation with the
National Center for Supercomputing Applications