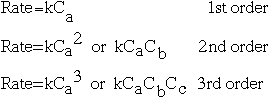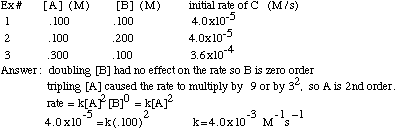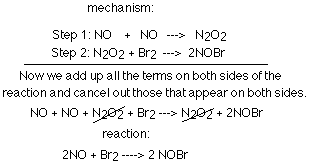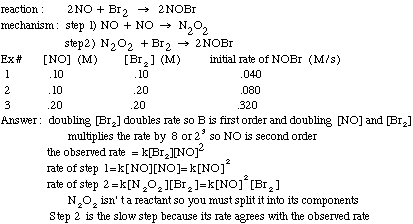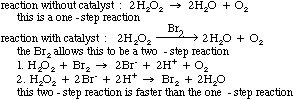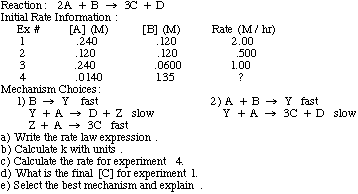
HOME
Course Chapters
Calculator Fundamentals
Mathematics Review
Basic Concepts
Advanced Concepts
Section Tests
Pre-test
Post-test
Useful Materials
Glossary
Online Calculators
Redox Calculator
Kinetics Arrhenius Calculator
Thermodynamics Calculator
Nuclear Decay Calculator
Linear Least Squares Regression
Newton's Method Equation Solver
Compressibility Calculator
Units Conversion Calculator
Nomenclature Calculator
Related Information Links
Texas Instruments Calculators
Casio Calculators
Sharp Calculators
Hewlett Packard Calculators
Credits
Contact Webmaster
|
Kinetics
Kinetics is the area of chemistry concerned with reaction rates. The rate can be expressed as:
rate = change in substance/time for change to occur (usually in M/s)
There are several factors that determine the rate of a specific reaction and those are expressed in the "collision theory" that states that for molecules to react, they must: - collide
- have the right energy
- have the right geometry
To increase the rate, you must make the above more likely to occur. This is possible by changing other factors such as:
- increasing the surface area (of solids)-this allows for more collisions and gives more molecules the right geometry
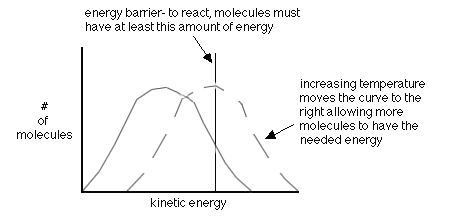
- increasing the temperature-this gives more molecules the right energy (also called the activation energy, Ea)
- increasing the concentration (of gases and solutions)-this allows for more collisions and more correct geometry
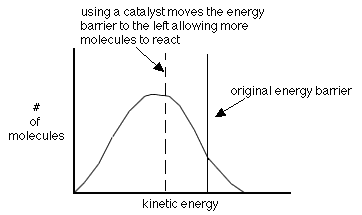
- using a catalyst-helps molecules achieve the correct geometry by providing a different way to react
The reaction rate can also be expressed by using a "rate law" and is written as follows:
For the general reaction: aA + bB + ... ----> gG + hH + .....
the reaction rate can be calculated by:
Reaction rate = k[A]m[B]n ....
Where:
[A], [B], etc. are the concentrations of the reactants
k is the rate constant or rate coefficient, a value dependent on
temperature.
m,n, etc. are exponents that correspond to a, b, etc. The concentration is raised to the power of its coefficient in the balanced equation.
Reaction order is a topic that comes with reaction rates. If you have a reaction in that A, B, and C are possible reactants, then we can describe the order of the reaction following this chart:
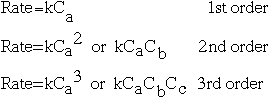
The order of the reaction is defined as the sum of the exponents of the coefficients. In general, first order reactions are most commonly seen, but reactions of other orders are also important. Zero-order reactions -- those for that the change in the reaction is independent of the concentration of the reaction -- are also possible.
It is possible to determine the order of a reactant, and eventually the reaction rate, using initial rate information that includes the concentration of the reactants and the rate at that the product is formed. If you double the concentration of reactant X and the rate increases by 2a, then the order of reactant X is "a". If you triple the concentration of reactant Y and the rate increases by 3b, then the order of Y is "b". For example, if you have a reaction with one reactant, A, and you double [A] and the rate doubles, then the rate=k[A]1.
If, instead, you double [A] and the rate quadruples, the rate=k[A]2. If you double [A] and the rate stays the same, then the rate=k[A]0.
To find the rate constant, k, using initial rate information, just plug in from the experiment one of the concentrations and rate into the rate law and solve. The units of k are trickier:
units of k=units of rate/(units of concentration)reaction order
Ex: for 2nd order reaction, k=(M/s)/M2=M-1s-1
Example Problem: Find the rate law and rate constant of A + B --> C using the following data
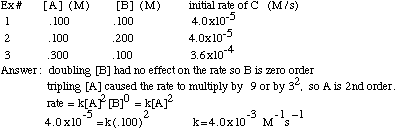
When dealing with reaction rates, it is sometimes important to know how to graph a straight line with the data you have. When graphing concentration versus time, there are two ways to graph a line. If you have a first order reaction, then the graph of ln[A] vs. time is a line. If you have a second order reaction, then the graph of 1/[A] vs. time produces a line.
A quantitative way to examine reaction rates is through Arrhenius Equation that states:
k=Ae-Ea/RT
Where:
A is a constant related to the geometry needed
e is a constant, approximately 2.7281
Ea is the activation energy
R is the gas law constant, 8.314 J/mol-K
T is the temperature in kelvins
If it is a simple geometry to attain, A will be large. If a large Ea is needed
then the exponent becomes more negative and therefore decreases k. If the temperature increases then the exponent becomes less negative and therefore increases k. A pop-up calculator is available to help practice using Arrhernius' Equation to make calculations.
The following are two (2) energy profile graphs that help demonstrate energy changes during a reaction.
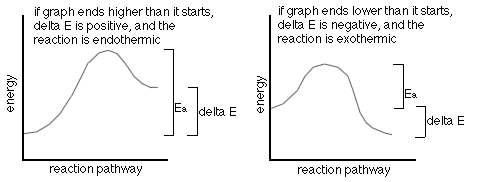
Not all reactions happen exactly as they are written. Most, in fact, go through an intermediate step.
Reaction mechanism studies look at how a reaction actually occurs.
Defined, a reaction mechanism is a series of elementary reactions that are
proposed to account for the rate law (kinetics) of a particular reaction.
The diagram below shows the two steps involved in a particular mechanism,
and it shows how we get the reaction from the mechanism.
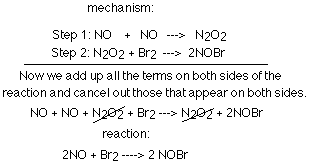
It is helpful to remember certain terms and facts when dealing with mechanisms.
You cannot derive a mechanism from the equation and when you combine the steps
of a mechanism, you end up with the reaction. The molecularity of a step tells
how many molecules are involved (most involve two (2) molecules so they are
bimolecular). An intermediate product is a molecule formed in one step and then used in another. One of the most important concepts to keep in mind is that the steps are not equally important. To speed up the reaction, you must speed up the slowest step (also called the rate-determining step).
rate law of slow step=rate law of reaction
When determining the rate of a step, simply make the exponent of the reactant's
concentration in the rate law the same as the coefficient of the reactant in
the step.
Example problem: Find the slow step of the following reaction mechanism
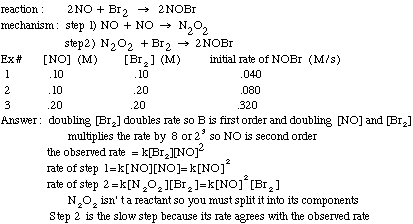
A catalyst is a substance added to a reaction that comes out of
the reaction unchanged. As mentioned earlier, catalysts help lower the activation energy as shown in the following graph. They do this by changing the reaction mechanism. 
The following is an example of how this can be done.
Practice Kinetic Quantitative Problem:
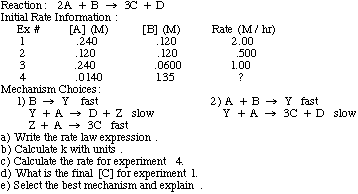 Kinetic quantitative solution.
Kinetic quantitative solution.
Practice Kinetic Qualitative Problems:
 Kinetic qualitative
solution.
Kinetic qualitative
solution.
[Advanced Index]
[Gas Laws]
[Thermodynamics]
[Kinetics]
[Equilibria]
[Redox Reactions]
[Nuclear Chemistry]
|

 Shodor
Shodor