Course Chapters
Section Tests
Online Calculators Linear Least Squares Regression Newton's Method Equation Solver
Related Information Links
|
Ratios and ProportionsKnowing how to work with ratios and proportions is very handy in chemistry classes, especially when working with different units of measurement. Let's start with some dictionary definitions:
So what are these things, really? Consider the following situation. In 1995, 78 women were enrolled in chemistry at a certain high school while 162 men were enrolled. What was the ratio of women to men? Men to women? Let's answer the questions using the definition of ratio. Filling in what we know:
men : women is 162:78 or 162/78 We could have reduced the fractions (cancelling out a factor of 6) or used our calculators to get a decimal equivalent for these fractions using the divide key:
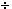 162 or
13 162 or
13 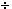 27 or .481481481 27 or .481481481 men : women is 162 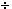 78 or
27 78 or
27 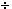 13 or 2.07692308 13 or 2.07692308 By writing the answer in these ways we have lost information, namely the specific number of men and women. Be careful! When given a ratio such as 13:27, the fractions may have been reduced so the original quantities could have been larger. This brings us to the idea of proportion. Ratios are said to be in proportion when their corresponding fractions are equal. What we really did above was notice that the fraction 78/162 was equal to the fraction 13/27 -- because we could divide both numbers in the first ratio by 6 to get the second ratio -- so the ratios are equal as well, i.e.,
These two equalities are examples of proportions (equal ratios); it is as simple as that. How are proportions used? Let's add another question to our problem: In 1996 the number of men enrolled was 193 while the ratio of women to men enrolled in chemistry stayed the about same as in 1995. How many women were enrolled in chemistry in 1996?
To answer this, we build a proportion equating the ratio of women to men in the two
years:
These are easiest to solve when written in fraction form. Notice that we've used
x for the unknown number of women since
it is common in algebra to use
the letter x as the variable. 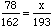
We can then use the
"cross-multiply" technique: So the number of women enrolled in 1996 was 92.9259259??? Use your common sense! There are no fractions of women walking around, so we will report 93 (rounding 92.9259259 correctly). It is probably wise to say "There are about 93 women enrolled in chemistry in 1996" since we were told the proportions were about the same. The issue of when to round will come up in chemistry, too. Often the objects being counted will be atoms or atomic particles like protons, neutrons and electrons; only whole number answers make sense in this case. Sometimes, however, we're measuring amounts (such as masses) which can be fractional. Then you should use the rules for correct rounding and significant figures reviewed in Session 1.
Try It Out
|
 Shodor
Shodorin cooperation with the Department of Chemistry,
The University of North Carolina at Chapel Hill
Copyright © 1996-2008 Shodor
Please direct questions and comments about this page to
WebMaster@shodor.org