Course Chapters
Section Tests
Online Calculators Linear Least Squares Regression Newton's Method Equation Solver
Related Information Links
|
Simple StatisticsThere are a wide variety of useful statistical tools that you will encounter in your chemical studies, and we wish to introduce some of them to you here. Many of the more advanced calculators have excellent statistical capabilities built into them, but the statistics we'll do here requires only basic calculator competence and capabilities.
Arithmetic Mean, Error, Percent Error, and Percent DeviationThe statistical tools you'll either love or hate! These are the calculations that most chemistry professors use to determine your grade in lab experiments, specifically percent error. Of all of the terms below, you are probably most familiar with "arithmetic mean", otherwise known as an "average".
A sample problem should make this all clear: in the lab, the boiling point of a liquid, which has a theoretical value of 54.0° C, was measured by a student four (4) times. Determine, for each measurement, the error, percent error, deviation, and percent deviation.
We show the calculations for the first data point as an example:
Standard DeviationStandard deviation is a particularly useful tool, perhaps not one that the professor necessarily will require you to calculate, but one that is useful to you in helping you judge the "spread-outness" of your data. Typically, you hope that your measurements are all pretty close together. The graph below is a generic plot of the standard deviation.
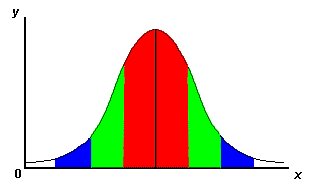 One standard deviation (sometimes expressed as "one sigma") away from the mean in either direction on the horizontal axis (the red area on the above graph) accounts for somewhere around 68 percent of the data points. Two standard deviations, or two sigmas, away from the mean (the red and green areas) account for roughly 95 percent of the data points. Three (3) standard deviations (the red, green and blue areas) account for about 99 percent of the data points. If this curve were flatter and more spread out, the standard deviation would have to be larger in order to account for those 68 percent or so of the points. That's why the standard deviation can tell you how spread out the examples in a set are from the mean. How do you calculate the standard deviation? It's not too difficult, but it IS tedious, unless you have a calculator that handles statistics. The formula for the standard deviation is as follows:
Basically, what this says is as follows:
If you have a statistics-capable calculator, this is really easy to do, since there is a button (usually labeled "SD") that allows you to do this. We, however, don't have a stats calculator (well, we do, but we're pretending!), so we have to do it the hard way. In this example, the student has measured the percentage of chlorine (Cl) in an experiment a total of five times. The arithmetic mean is calculated to be 19.71. The student wants to find out the standard deviation for the data set, with particular interest in the range of values from one sigma below the mean to one sigma above the mean:
Adding up all of the d2= 0.0342 This means that the standard deviation for this problem is 0.09, and that if we keep doing the experiment, most (68% or so) of the data points should be between 19.62 (19.71 - 0.09) and 19.80 (19.71+0.09). The lower the standard deviation, the better (in this case) the measurements are.
Try It Out
[Units, Dimensions, and Conversions] [Percents] [Simple Statistics] [Logarithms] |
 Shodor
Shodorin cooperation with the Department of Chemistry,
The University of North Carolina at Chapel Hill
Copyright © 1996-2008 Shodor
Please direct questions and comments about this page to
WebMaster@shodor.org