Course Chapters
Section Tests
Online Calculators Linear Least Squares Regression Newton's Method Equation Solver
Related Information Links
|
Periodic Table
The Bohr theory for a hydrogen-like atom or ion (an atom or ion containing a nucleus and only one electron, e.g., H, He+, Li2+ and Be3+) gives the energy of the electron in a given electron shell as E being inversely proportional to n2 and the radius of the shell as r being directly proportional to n2 where n is the principal quantum number. For a hydrogen-like electron system, the energies of the subshells depend only on the principal quantum number 1s < 2s = 2p <3s = 3p = 3d < 4s = 4p = 4d = 4f < ... However, for a multielectron atom or ion (an atom or ion containing a nucleus and more than one electron), the energies of the subshells are no longer the same because of the various electron-electron interactions and generally follow the order 1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f ≈ 5d < 6p < 7s < 5f ≈ 6d < 7p < ... Each s subshell contains one s orbital, each p subshell contains three p orbitals, each d subshell contains five d orbtials, each f subshell contains seven f orbitals, etc., and each orbital can be assigned a maximum of two electrons. The lowest energy state (the ground state) of an atom or ion is the one in which all electrons are assigned to the lowest available orbitals. For example, using the above filling order we would write the electron configuration for the 10 electrons in neon as Ne 1s2 2s2 2p6 and the 40 electrons in zirconium as Zr 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d2 Example Problem: Write the electron configuration for the ground state of an atom of arsenic (Z = 33). Answer: For the 33 electrons As 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p3 Note that the sum of the numbers of electrons in each subshell is equal to the total number of electrons present in the atom or ion. Note that there are some discrepancies between the predicted configurations based on the above general filling order and the observed electron configurations–particularly for the transition (d-block) elements and the inner transition (f-block) elements. We will not concern ourselves with these in this review. Periodic Trends in Electron Configurations The arrangement of the atoms in the standard periodic table is based on the electron configurations. The atoms in a periodic table family or group (a vertical column of elements) will all have the same valence (outer) electron configurations with respect to the subshells involved. For example, all of the halogens in Group 17 will have the ns2 np5 configuration–only the values of the principal quantum number change. These outer configurations are summarized in the figure. 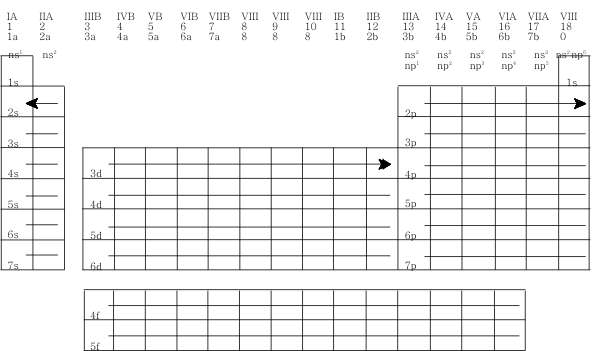 Periodic Trends in Oxidation Numbers Most atoms do not have completely filled subshells and will gain, lose, or share electrons with other atoms to “complete” these subshells. For example, the metals in Groups 1 and 2 readily form positively charged ions (cations) resulting from the loss of the nsx electrons Na(1s2 2s2 2p6 3s1) → Na+(1s2 2s2 2p6) + e-
Ca(1s2 2s2 2p6 3s2 3p6 4s2) → Ca2+(1s2 2s2 2p6 3s2 3p6) + 2 e-
The nonmetals in Groups 13-17 form negatively charged ions (anions) resulting from the gaining electrons to completely fill the np subshell O(1s2 2s2 2p4) + 2 e- → O2-(1s2 2s2 2p6) Br(1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p5) + e- → Br-(1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6)
For ions, the oxidation number is equal to the charge on the ion. In compounds where electrons are shared, the nonmetals can also be assigned positive oxidation numbers corresponding to the loss of the npx and the nsx electrons. For example, in various compounds of sulfur, S (1s2 2s2 2p6 3s2 3p4), sulfur is often considered to have a +4 oxidation number from the “loss” of the 3p4 electrons and a +6 oxidation number from the additional “loss” of the 3s2 electrons. To predict the oxidation number of the transition and inner transition elements is a little more tricky. Even though we would write the configuration of vanadium based on the filling order as V 1s2 2s2 2p6 3s2 3p6 4s2 3d3 we must rewrite the configuration as V 1s2 2s2 2p6 3s2 3p6 3d3 4s2 with the electron occupancy placed in order by increasing principal quantum number which represents the order of removing electrons. The first electrons that are removed are from the greatest principal quantum number V2+ 1s2 2s2 2p6 3s2 3p6 3d3 followed by some or all of the electrons in any partially filled subshell V5+ 1s2 2s2 2p6 3s2 3p6 Because some of the subshells for transition and inner transition metals are close in energy, there are often several different possible oxidation numbers. 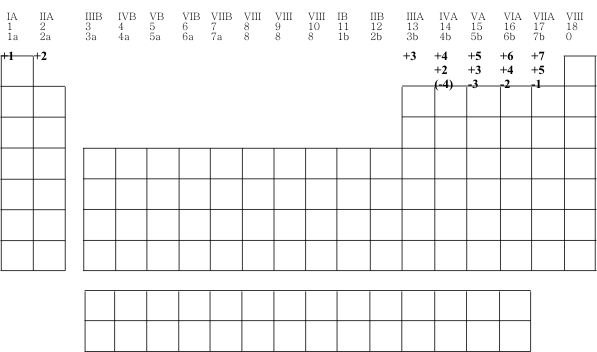 In going down a family of elements, both the nuclear charges and principal quantum numbers increase as the atomic numbers increase. As the nuclear charges increase, the atomic radii are predicted to be smaller because of the greater positive electrical charges of the nuclei attracting the electrons. From the relationship that r is directly proportional to n2, we would predict that the atomic radii should increase as the principal quantum numbers increase. These are opposing effects as the atomic numbers increase. The greater effect is from the increasing principal quantum number–however, the predicted increases are not as large as expected because some of the increase is offset by the increasing nuclear charge. The general trend is that atomic radii increase within a family with increasing atomic number. In going across a period (a horizontal row) in the periodic table, the valence electrons of the elements all have the same principal quantum number and so we would predict no change in the radii from a change in the value of n. However, the nuclear charges increase as the atomic numbers increase and this effect tends to decrease the size of the atoms. The general trend is that atomic radii decrease within a period with increasing atomic number. The radii of elements that follow the transition or inner transition elements are similar to those directly above them in the periodic table family because of the effect of the additional number of elements in these longer periods offsetting the increased value of the principal quantum number.  All of the following trends in atomic properties are directly related to the trends in atomic radii. Periodic Trends in Ionization Energy The first ionization energy (ionization potential) is the energy change for the removal of the least “tightly” bound electron for a gaseous atom Na(g) → Na+(g) + e- Ionization energies are always endothermic. Because Coulomb’s law (E is inversely proportional to r) predicts that it is easier to remove an electron from a large atom than from a small atom, the ionization energy is predicted to decrease within a family with increasing atomic number because the size increases and is predicted to increase across a period with increasing atomic number because the size decreases. 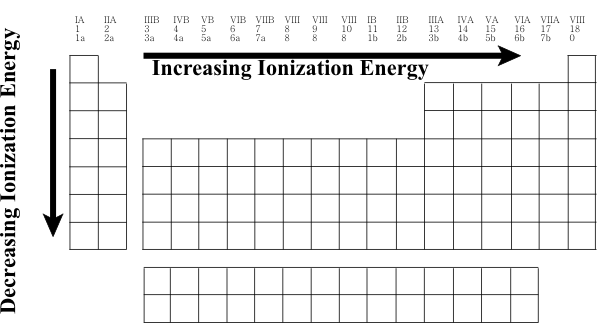 Periodic Trends in Electron Affinity The electron affinity is the energy change for the addition of one electron to a gaseous atom Cl(g) + e- → Cl-(g) Values of electron affinities can be either endothermic or exothermic. If the electron configuration is “stable” before the process, e.g., ns2 or ns2 np6, then the process is endothermic and if the configuration ns2 np3, the process is not as exothermic as expected. Excluding these exceptions, the general trend for the exothermic process based on Coulomb’s law (E is inversely proportional to r) predicts that the electron affinity will decrease within a family with increasing atomic number because the atoms increase in size and will increase across a period with increasing atomic number because the atoms decrease in size. 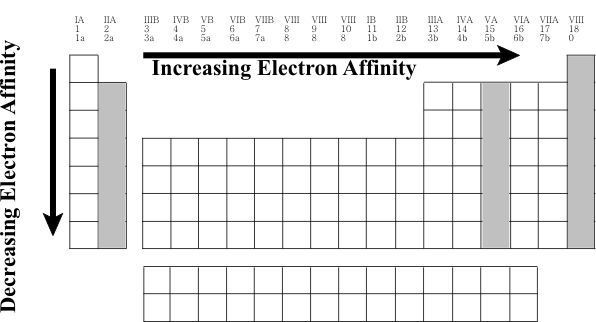 Periodic Trends of Electronegativity Electronegativity is the “ability” of an atom in a covalent bond to attract electrons to itself and is related to the ionization energy and electron affinity of the atom. There are several different methods of assigning numerical values for this property, but the general trends are that the electronegativity decreases within a family with increasing atomic number and increases across a period with increasing atomic number. 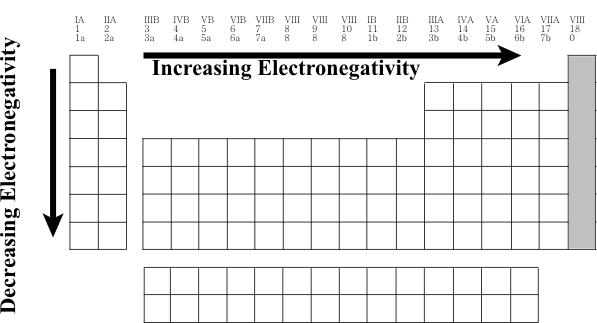 Try It Out 1. Write the complete electron configuration for B, P, Ti, Ge, and U. 2. Predict the oxidation numbers for the elements in question #1. 3. Choose the larger atom in each pair: Mg, Ca; Be, F; Cl, Br; S, Cl. 4. Choose the element with the greater ionization energy in each pair: Mg, Ca; Be, F; Cl, Br; S, Cl. 5. Choose the element with the greater electron affinity in each pair: Be, F; Cl, Br; S, Cl. 6. Choose the more electronegative element in each pair: Mg, Ca; Be, F; Cl, Br; S, Cl. Additional Information Available on the Web http://www.lynchburg.net/hhs/chemistry/trends http://dl.clackamas.cc.or.us/ch104-06/periodic.htm http://periodic.lanl.gov/default.htm
[Basic Index]
[Chemical Nomenclature]
[Atomic Structure]
[Periodic Table] |
 Shodor
Shodorin cooperation with the Department of Chemistry,
The University of North Carolina at Chapel Hill
Copyright © 1996-2008 Shodor
Last Update: Sunday, 06-Oct-2002 13:08:39 EDT
Please direct questions and comments about this page to
WebMaster@shodor.org