Stimulating Understanding of Computational science through Collaboration, Exploration, Experiment, and Discovery for students with Hearing Impairments
a collaboration of the Shodor Education Foundation, Inc., Eastern North Carolina School for the Deaf, Barton College, the National Technical Institute for the Deaf, and Interpreters, Inc.

For Teachers!

Flu Model

Notes on teaching the lesson: This lesson allows the students to explore some of the factors that affect the spread of a flu outbreak. The lesson uses an SIR model. An SIR model monitors the changes in the three groups of people (Susceptible, Infected, Recovered) as the illness moves through the population. 

 This lesson is designed to help the students learn that science and computer models are valuable tools for solving real-life issues. Using science allows the students to understand what happens and how it happens. From a societal standpoint the value of science is in how we use this understanding. By applying their understanding of the dynamics of a flu outbreak to a company's sick leave and vaccination policy the students can see how science can be used to enrich their lives and pocketbooks. 

The second important issue introduced in this model is the assumptions that are made. Scientific assumptions aren't guesses. They are the modifications and simplifications that we include in a model that we know aren't exactly representative of the real situation. To include all of the possible variables and their interactions in the model would make it so large and unwieldy that it wouldn't be practical to use. As an example, the virulence factor is a combination of 2 factors. First, a contagious person exposes, say, 40 people. Second, these 40 people each have a chance of contracting the flu, say, a 5% chance. The SIR model combines these 2 variables. Further, my example of 40 is only an average number. Some countries have good infrastructure and thus extensive transportation and mixing of individuals. Other countries are poorer and very rural in nature. These countries have less mixing and a lower density. These factors combine to produce a lower number of exposures for one infected person. Likewise the exposed people don't all have the same natural resistance to the flu. Some old or stressed individuals are more susceptible. Some communities have a better diet and are more physically active. Others are composed of couch potatoes who eat snack foods. Some communities have good health care and sanitation, which reduces the general health stress on its individuals.  The model's virulence factor uses an average value. By assuming an virulence factor of 2 we acknowledge that it isn't technically correct for all communities, but for the purposes of this model, it is an acceptable first approximation. Later the model can be refined by reworking the assumptions to get results that more accurately represent particular situations. 

Models by their nature are simplifications of a situation so they will always have some assumptions. As scientists it is important that we identify the assumptions we make. This allows others to evaluate our results and think of new questions and approaches to the issue at hand. 

The following are the student pages. Answers and suggestion for the teacher are in BLUE.

The SIR Model

Analysis

Ask your teacher if you will be using the Stella model or the Java version.

If you are using the Stella model, set these initial conditions: 
exposure rate = .5 
input contagious=1 
days contagious=3 
vaccination rate=0 

Open the stock graph and click on the runner in the lower left corner of the page.

If you are using the Java model, set these initial conditions: 
contagious=1 
recovered=0 
susceptible=1000 
days contagious=3 
exposure rate=.5 

These values create a population of 1001 people. At the beginning of the run only one person is sick. Sick people
can spread the flu for 3 days on average.

Explain what happens to the people. 
How many get sick? 586 have been sick and recovered at the end of the run. I rounded off the answer. The two models don't give exactly the same answers. Why??? It is important for the students to realize that numbers in science aren't the same as numbers in math. In science we have uncertainty in our measurements. When we use computers to do the math for us, additional variations can creep in. Computers do the math in binary, so the round off of fractional remainders is different. The two models translate their directions for the computer in slightly different ways. When those operations are repeated hundreds of times, slightly different answers can occur. In this case the difference isn't significant. Computer modelers need to check that trends in their data are reasonable and not artifacts of their computer's math chip or processing technique. 
How many never get sick? 416 for the Stella model and 415 for the Java model. 
How does the number of sick people change over time? The number of sick people starts at 1 and rises to 49 by day 32. By day 70 the number of sick people has returned to 1. It continues to slowly fall after that. The shape of the curve is normal i.e. a bell curve.
Describe the contagious curve. Describe the slope of the contagious curve's different sections. The curve is shaped like a bell, i.e. a normal distribution. The curve starts with a gradually increasing positive slope then rapidly increases to a stable section with a slope of about 3. Then the slope decreases to a slope of 0 at about 30. The second half of the curve mirrors the first half. the slope continues to decrease until it reaches a stable section with a slope of approximately -3. Then the slope increases to 0 where it ends.
What is happening to the number of contagious people at different parts of the contagious curve? Relate these
changes to the slope of the curve at each part. The number of contagious people starts at one and rises slowly at first. In this section the slope is small but increasing. When the curve becomes nearly linear at a slope of approximately 3, the number of contagious people is rising at a steady rate of about 2 additional contagious people per day. When the curve levels off and the slope becomes 0, the number of contagious people reaches a peak at 64.48. When the curve become negative, the number of contagious people starts to decline. Initially, the negative slope is small and the decrease in number of contagious people small. When the slope is approximately - 3, the number of contagious people decreases by about 3 people per day. When the slope is returning to 0 the number and decrease in the number of contagious people becomes very small.

To see the numerical data on the Java model click the text output button. That opens a window with 4 columns of numbers. The first column is the day. The second column is the number of contagious people. The third column is the number of recovered people. The fourth column is the number of susceptible people. You can copy and paste this data into an Excel spreadsheet.

To see the numerical data on the Stella model, click on the graph. Values appear for each variable. As you drag the cursor across the graph you can see the values for different days. By clicking off of the graph the graph closes. If you open the Table 1 icon a table of the data appears. This data can be copied and pasted onto an Excel spreadsheet.

Consider the formula that moves people from the susceptible stock to the infected stock. People moved =
susceptible*contagious*infection_rate. The infection rate = the virulence factor / total population. Thus the full
formula is People get sick = susceptible*contagious* virulence factor / total population.

Use the get sick formula to explain the change in the contagious stock. The virulence factor and the total population don't change, so they don't contribute directly to a change in direction of the contagious stock. Initially, the susceptible is large and the contagious is small. The large susceptible value causes a rise in the number of contagious. With an increase in the number of contagious, the people getting sick rises even more, which causes even more to get sick. As this proceeds, the number of susceptible decreases. This increasing contagious and decreasing susceptible results in a relatively stable growth. All along, the contagious are becoming recovered at a steady rate. Eventually, the susceptible decreases to the point that the number that are recovering is greater than the number that are getting sick. At this point, the contagious is also decreasing, and we see a rapid decline in the number getting sick because both the susceptible and contagious are declining. As the number of people getting sick decreases, the rate at which susceptible people get sick decreases so the number of susceptible begins to level off. This causes the population to stabilize as the number of contagious approaches 0.

With a little algebra manipulation, the equation becomes People get sick = contagious*virulence factor*(susceptible/total population). This rearrangement of the formula allows us to have a different conceptual understanding of the dynamics. If the virulence factor is 2, then each contagious person will make 2 susceptible people sick. That is the case if nearly everyone is susceptible. If a contagious person exposes 40 susceptible people and there is a 5% chance that an exposed person will get sick, then 2 people get sick. If half of the people are recovered, then the contagious person exposes 20 susceptible and 20 recovered people. The recovered can't get sick. The 20 susceptible people each have a 5% chance of getting sick. That means that 1 person gets sick, not 2. Thus the formula means that the number of people who get sick equals the number of contagious people times the number of people one contagious person infects times the fraction of people that are susceptible. Initially, the number of contagious people increases because the fraction of susceptible is close to 1. As time goes on, the fraction of the people that can become infected decreases, so the number of contagious levels off and then declines. When the number of contagious reaches 0, the outbreak dies out.

The first explanation come, from a standard way to model an interaction between 2 groups. How many ways can 2 groups interact or combine? Multiply them together. Then multiply that by the rate at which these interactions successfully produce the desired effect. Mathematically, this is the same as the second explanation. It is valuable for students to see that a few basic relationships can be combined to produce the models we use. They can also see that there is more than one correct way to do math and thus explain its real world application.     

Models allow you to explore different scenarios. How would the flu spread if a bus full of sick people came to town? Use the contagious slider to systematically evaluate the effect of changing this variable.

Do the shapes of the curves change? The basic shape doesn't change. The curve becomes slightly skewed. With more sick people to start with, the outbreak runs its course a little faster and the number of sick reaches a slightly number.
Does this have a large or small net effect on the number of people that get sick. The effect is relatively small considering the large relative change in the number of sick people.
Propose an explanation for the size of effect you observed. The dynamics of the larger initial infected run are very similar to the run starting with 1 infected except that you don't start on day, one but rather a week or two into the run. Once the small starting run catches up, they behave about the same. Since the large number of contagious occurs with slightly more susceptible there are a few more recovered at the end of the run. 

Epidemiologists have studied flu outbreaks. The following data shows the percentage of people that stay home by the third day of the flu. 
Preschoolers 80% 
school age 75% 
adults 50% 

Employers have policies on sick leave. One company only pays people who come to work. If you are sick and stay home you don't get paid. Other companies give their employees 2 weeks of paid sick leave. They are telling their people, "If you don't feel well, stay home so you don't make us sick!"

This model keeps track of the lost productivity due to illness. If people stay home sick the company looses one day of productivity. If employees work when they are sick they get some work done. The model calculates a 30% reduction in productivity for each day worked by a sick person. A person is sick for 7 days in the simulation.

Adjust the "days contagious" slider to simulate different sick leave policies. The "lost productivity" graph displays the number of work days lost.

Compare the number of people who get sick under different policies. Under a policy that only pays employees who come to work, the average worker would work more than 3 days while contagious, perhaps 5 or 6 days. In a company that gives sick leave, the average worker may only work 2 or 3 days while they are contagious, thus reducing the model's days contagious value. The following graph depicts the lost productive days and the number of people that were sick for different values of the days contagious slider. Input contagious is set at 1, Vaccination rate is set at 0, exposure rate is set at .5, days contagious varies from 1 to 7. The data comes from the Stella model.

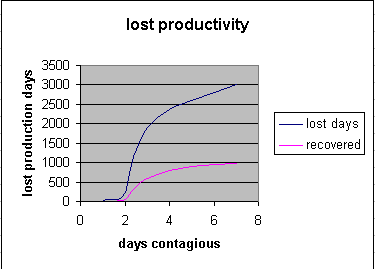
At 2 days contagious there is a dramatic reduction in lost production and number of sick people. Ideally the  company should try to get the members of the community to stay home for all but 2 days of an illness. If one company has a policy encouraging it's employees to stay home, but their spouses' and children's associates don't share the ethic, then it may be less effective.     
Compare the amount of lost productivity under different policies. "Contagious" is an Excel spreadsheet with the data for the lost production days and recovered (number of people that got sick) for runs of the model with varying days contagious.  

In the above scenario everyone followed the incentives of the sick leave policy. A real community has different employers, school children, retired people etc.

How would you adjust your variables to reflect a more realistic community? The days contagious for the community should be adjusted toward the community average of about 3 days. Depending on the relative size of the company and the community the adjustment will vary.
If you are using the Stella model, suggest improvements to the model. Answers will vary. A parallel sub- model represent the employees could be added within the model to allow them to have a slightly different behavior. 
Based on your findings, make a recommended sick leave policy for the company. Answers will vary. A policy encouraging people to stay home when ill could be effective in reducing the amount of illness and lost productivity if the community leaders i.e. Mayor, Chamber of Commerce, clergy and educators enthusiastically support and promote it. The community needs to reduce the amount of time an average sick person is out spreading the flu or a cold by about one day. Ask the students if they think this is a practical goal.

The model can simulate people getting flu shots. Your company wants you to recommend a vaccination policy. Flu shots cost $10 per person. A day of lost productivity costs the company $100. The employees of your company are 10% of the community. Employees call in sick when their children are sick. Employees and their dependents make up 30% of the community.

You job is to determine if it would be cost effective to vaccinate some or all of the employees or the community. "Vaccination" is an Excel spreadsheet of the productivity costs for vaccination rates from 0% to 80%. The other variables were held constant at the levels suggested at the beginning of the analysis page. If employees are 10 % of the community, then the company absorbs 10% of the lost productivity costs, or $18,950. If we assume that parents stay home with their sick children, then this number may be about twice this high. The cost of vaccinating all of the employees is $1,000. This saves the community $51,400. The employees won't get sick, but if they stay home with sick family members, the company could still loose $10,000 to $20,000. The company saves $18,950 because their employees aren't sick and a little bit more because their families aren't exposed to a sick parent.

The cost of vaccinating the employees and their families is $10 X 300 = $3,000. This protects the company from productivity losses and saves it at least $18,950. That is cost effective. Vaccinating 30% of the community also reduces the community's loss by $162,800. If some of the other employers join the program and vaccinate an additional 10% of the community then the productivity costs are reduced to $2,500 for the entire community. The total cost of the vaccinations is only $4,000. Additional vaccinations beyond 40% aren't cost effective. In reality the shots aren't 100% effective; estimates are around 90% effective. Also, sometimes an unanticipated virus appears that the shots don't address. For this exercise we are assuming 100% protection. A community might shoot for a 50% vaccination rate. That would protect people whose shot didn't take. The protection of the 50% that aren't vaccinated is called herd immunity. Some people refuse to get vaccinated for religious reasons or special health reasons. If enough of the population is vaccinated, the unvaccinated people are also protected. Some companies are starting to offer flu shots to their employees because of these findings.

Flu shots don't protect from the common cold and other diseases. A policy that encourages both flu shots and people staying home when sick to reduce the spread of disease may be advisable. Companies would need to do their own analysis based on the importance of lost production versus out of pocket expense for sick leave. Companies also need to consider ways to reduce the abuse of sick leave.  

Instructions for simulating vaccinations using the Java model: 
Adjust the recovered and susceptible sliders. Example, for a 10% vaccination rate set the recovered to 100 and the susceptible to 900. Then run the model.

Instructions for simulating vaccinations using the Stella model: 
Adjust the vaccination rate slider. Example, for a 10% vaccination rate set the slider at .10.

If you have STELLA at your school and made improvements to my model please email them to me so I can post them, or post them yourself and let me know so I can link to your page. 

Developed by
The Shodor Education Foundation, Inc.

Copyright © 1999-2001 by The Shodor Education Foundation, Inc.

This project is supported, in part, by the National Science Foundation Opinions expressed are those of the authors and not necessarily those of the National Science Foundation.