Course Chapters
Section Tests
Online Calculators Linear Least Squares Regression Newton's Method Equation Solver
Related Information Links
|
Problem 1 SolutionFind the missing quanity in each of the following: a. What is 10% of 672.3 kg? b. 42 is what percent of 132.3 g? c. 18.7 is .5% of what amount?
(a) 67.23 kg (b) 32% (c) 3740 g Solution Steps for Part (a):What is 10% of 672.3 kg?
Answer:We'll use the clues from the statement:What is 10% of 672.3 x = .10 * 672.3 Multiplying on a calculator gives x = 67.23. What about significant digits? We'll assume that the percent was not obtained from a measurement, i.e., it is exactly right. So the number of sig figs is determined by the 672.3 to be four. How do you decide whether a number as stated is exact, in general? Think about the problem that you are working on in each case, and use your common sense! What about the units? Percents are dimensionless numbers and the units on the right hand side are kg, so the units on the left must be kg as well! What is a dimensionless number??? A number with no associated units. Why are percents dimensionless??? Well, if we go back to the "part out of the whole" idea of a percent, whatever the units are on "the part" must also be the units on "the whole" so the units will always cancel out. Watch:
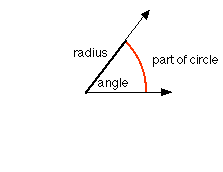
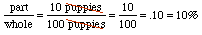 Another common dimensionless number is an angle measurement in radians -- just as with percents the units cancel! An angle measurement given in radians:
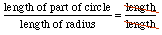  Solution Steps for Part (b):42 g is what percent of 132.3 g?
Answer:We'll use the clues from the statement:42 is what% of 132.2 42 = x * 132.2 Dividing by 132.2 gives x = .31770045 = 31.770045%. Sig figs?? Well that depends on which numbers were measurements; if we assume that 42 and 132.2 were, we should state the answer with 2: x = 32%, Solution Steps for Part (c):18.7 g is .5% of what amount?
Answer:We'll use the clues from the statement:18.7 is .5% of what 18.7 = .005 * x Dividing by .005 gives x = 3740; the units are grams. |
 Shodor
Shodorin cooperation with the Department of Chemistry,
The University of North Carolina at Chapel Hill
Copyright © 1996-2008 Shodor
Please direct questions and comments about this page to
WebMaster@shodor.org