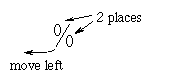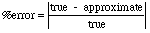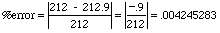
HOME
Course Chapters
Calculator Fundamentals
Mathematics Review
Basic Concepts
Advanced Concepts
Section Tests
Pre-test
Post-test
Useful Materials
Glossary
Online Calculators
Redox Calculator
Kinetics Arrhenius Calculator
Thermodynamics Calculator
Nuclear Decay Calculator
Linear Least Squares Regression
Newton's Method Equation Solver
Compressibility Calculator
Units Conversion Calculator
Nomenclature Calculator
Related Information Links
Texas Instruments Calculators
Casio Calculators
Sharp Calculators
Hewlett Packard Calculators
Credits
Credits
Contact Webmaster
|
Percents
Most students learn to use percents in middle school, but many
people still have trouble interpreting information involving
percents even as adults. Just what is a percent (%)?
The word
percent comes from the Latin per centum meaning
"out of one hundred," so we can think of 22% as "22 out of 100." Thus
a percent is a symbol representing a ratio of the part -- in this
case 22 -- to the whole -- 100.
A percent must be changed to a number (fraction or decimal) before we
can compute with it. Hence 22% is the ratio 22 : 100, which gives:
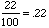 Other examples:
Other examples:
| percent notation |
ratio notation |
number notation |
| 30% |
30 : 100 |
30 / 100 = .3 |
| 8% |
8 : 100 |
8 / 100 = .08 |
| 63.7% |
63.7 : 100 |
63.7 / 100 = .637 |
| 100% |
100 : 100 |
100 / 100 = 1 |
| 212% |
212 : 100 |
212 / 100 = 2.12 |
| 5 3/4% |
5 3/4 : 100 or 5.75 : 100 |
5.75 / 100 = .0575 |
We will most often use the decimal form (in bold above) because it is
easy to find on a calculator by dividing by 100. Let's make some notes
from these examples.
- The mechanics of changing a percent to a decimal number
involves moving the decimal point two places to the left. The percent
symbol can help us remember this:
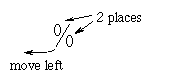
- When we change percents smaller than 10 percent to numbers,
we need to place holding 0s -- as with 8% and 5 3/4%.
- 100% is 1, reinforcing the idea that x% describes x's
part of "the whole."
- Percents representing more than 1 are possible (212%) -- they
are used to talk about something growing really large rather than as
"part out of the whole."
Before looking at how percents come up in science, we need to
be able to answer questions like those below. Click on the question
to look at how to find the answer. We give several tips on using percents
on these pages, so you might want to look even if you got the answer right!
What is 20% of 35? It's 7.
11 is what percent of 20? It's
55%.
6.5% of what number is 80.02? It's
1231.076923 (or 1200 to two sig figs).
What is 10 after
being increased by 15% ? It's 11.5.
What is 201.1 after being decreased
by 25% ? It's 150.825.
Percents come up several
times in chemistry. Remember that the key is to change a percent
to a number
before calculating with it and, if the answer is to be stated as a percent, convert the
number to a percent before giving the answer.
So what else do you need to know to be ready for chemistry?
- When measuring a sample for its constituent parts, the amounts of each
part
are often stated as %s -- you'll see this in percent abundance of isotopes and in
percent composition of compounds. Don't forget: part / whole.
For example:
A sample of lead was tested in a mass spectrometer, and four isotopes
were found along with their % abundances:
204 at 1.4%, 206 at 24.1%, 207 at 22.1% and 208 at 52.4%.
How do we read these? 1.4% of the sample was isotope 204, 24.1% of
the sample was 206, etc. Notice that the percents add up to 100. (All
the parts together should total up to the whole!)
- When conducting an experiment to synthesize a chemical compound, you'll
compare the amount you should get (according to the theory of how
chemicals bind together) to the actual amount you
did get from your experiment --
percent yield = experiment / theory.
For example:
Suppose we know that if we take formic acid and
geraniol, we can make a synthetic rose perfume. If we start with
1000.0 g of geraniol added to formic acid, the theory of chemical
reactions (stoichiometry!) can be used to calculate
a theoretical yield of 1182.2 g of the rose essence.
Our experiment actually produces 871.2 g. What is the percent yield?
experiment / theory = 871.2 / 1182.2 = .736931145 = 73.69% to four sig figs.
- When working with measurements there is often some associated error
-- usually measured as
percent error:
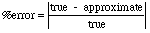
For example, suppose we test a new thermometer for accuracy by using it to find the boiling point
of pure water.
The boiling point of pure water is 212°F but the thermometer measures
212.9°F. What is the % error of the reading?
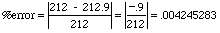
which is .425% to
three sig figs. Note the absolute values; that's why the - sign was dropped.
Try It Out
-
Find the missing quantity in each of the following:
- (a)
- What is 10% of 672.3 kg?
- (b)
- 42 is what percent of 132.3 g?
- (c)
- 18.7 g is .5% of what amount?
Check your work.
-
In 80.043 g (1 mole) of ammonium nitrate (bomb city!), there are 28.014 g
of nitrogen, 47.997 g oxygen and the rest is hydrogen.
- (a)
- What percent of ammonium nitrate is nitrogen?
- (b)
- What percent of ammonium nitrate is oxygen?
- (c)
- What percent of ammonium nitrate is hydrogen?
Check your work.
-
We performed an experiment in which the theoretical yield of the
desired chemical is 143.2 liters. If the percent yield of the actual
experiment is 62%, how much of the chemical did we really end up with?
Check your work.
-
A sample thought to be caffeine is tested and the resulting composition
was 53% carbon, 4% hydrogen, 30% nitrogen and 13% oxygen. We know
from theory that one mole of caffeine contains 96.08 g carbon,
10.08 g hydrogen, 56.04 g nitrogen and 32.00 g oxygen. Was the sample
really caffeine?
Check your work.
|

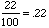
 Shodor
Shodor