The purpose of this Web site is to provide students and their teachers with an appropriate and authentic resource with which to study the effect of soil types, ground cover, and other variables on the amount, or quantity, of surface water runoff.
The amount of runoff for differing conditions can be modeled
through the use of the information on these pages and the "runnable", or interactive, model that accompanies these materials. The model allows for the
modification of such variables as soil type, ground cover type, and rain duration in order for the user to obtain a greater understanding of the quantity of water runoff and the effect of different soil and cover types on the water runoff.
Why is such a model appropriate and authentic? The interactive model provided here is appropriate because it uses the right technology -- the study of science through its representation in mathematical language and implemented on a computer -- to understand a complex problem that is exceptionally difficult to study "in the field." Most schools, students, and educators do not have the resources or expertise to conduct meaningful studies of surface water runoff in their communities. It is appropriate because a solid understanding of the scientific, economic, and political impact of surface water runoff is critical for all citizens. This is especially important for states like North Carolina, where water runoff has significant implications for farmers, homeowners, and those who are concerned about the quality of bodies of water such as the Neuse River.
The model is authentic because the science and mathematics that provide the foundation of the model are the exact same as those used by research scientists. The equations and values used in this model come from the U.S. Department of Agriculture Soil Conservation Service (SCS). All of the equations for this model come from Publication 210-VI-TR-55, Second Edition, 1986. The use of these equations and parameters allows us to put a scientifically-accepted computational tool into the hands of "young" scientists and their teachers. While the scenarios may be developed for educational purpose, the mathematical and computational tools are authentic.
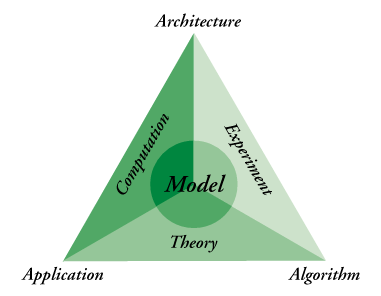
The model uses the conceptual framework of computational science -- application,
algorithm, and architecture. The application
refers to the scientific problem of interest and the components of that problem
that we wish to study and/or include. Like the three parts of the "fire triangle -- a source of fuel, a source of a spark, and oxygen -- computational models require and understanding and an implementation of application, algorithm, and architecture. The model is also defined by what we know from theory, from experiement, and from computation. Old and new theories suggest experiments, which suggest computaions, which suggest refinements to the theory and ideas for new experiments:
Computational science is an important method for teaching and learning science. Many of the really interesting events of science are those that are difficult to study experimentally because they:
- occur too quickly (such as molecular interactions in chemistry)
- occur too slowly (such as population dynamics)
- are too costly to replicate in the laboratory (wind tunnel modeling)
- are too dangerous (rapid combustion experiments)
With computational science, not only can the events be simulated, but also the experimental variables can be modified and the event can be re-enacted to observe the effect. This is an exciting and empowering hands-on process of learning that gives the students rapid feedback on their experiments and helps to develop scientific intuition.
Computational science has been defined in many ways. We define it as the correct and efficient match of application, algorithm, and architecture which enables one to do science or engineering on a computer.
The application is simply a concise statement of the problem to be solved. Computational methods are being applied to all areas of study, not just the physical sciences. Typical applications include the changing of voting habits, effects of atmospheric pollutants, the formation of galaxies, the dynamics of world economies, the erosion of beaches, or the modes of vibration in a molecule. The use of models in the political and social sciences is becoming increasingly important at all levels. In short, appropriate applications cross all traditional boundaries and disciplines.
Once we have an application to be studied, we must translate that problem into a mathematical format, known as the algorithm.
The final part of the model is the architecture. The mathematical representation (the algorithm) must be converted into some appropriate computer code using some programming language, and then be run on some piece of hardware. A big challenge in learning to do computational science is choosing the appropriate tools for a particular problem. One does not need to know FORTRAN (a high-level programming language) that runs on an expensive supercomputer to simulate a simple flu epidemic! The student needs to begin to understand the strengths and weaknesses of various computational tools, and the impact they play on answering the key question that all computational scientists ask:
How do we know the model is right?
|

