We can look at the change in concentrations of NO, NO2, and CO over time with this system of first-ordered differential equations. In the schematic below, we show the reactions by number from the graphic above. For example, R1 represents the photochemical reaction in which light energy hits a molecule of NO2 to form NO and singlet oxygen:
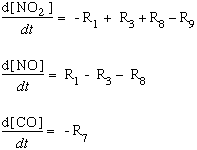
In the equations below, we substitute the kinetic components for each of the values
of R:
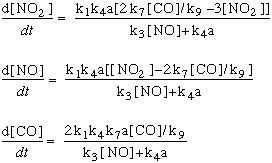
In these equations, the term "k" refers to the rate constants, and are numbered following
the reaction numbers in the graphic above.
We wish to develop an algorithm to evaluate the photooxidation of CO in the presence of NOx. Equations can be derived for [NO2], [NO], and [CO], where the brackets [ ] mean the concentration of the species. Once developed, we need to integrate these equations numerically for the following sets of conditons and plot [NO2], [NO], [CO], and [O3] in parts per billion (ppb) as a function of time from t=0 to t=180 minutes with a time step around 0.1 min
for a stable solution. Integration of these differential equations requires the use of some numerical method, such as Euler's method or one of several Runge-Kutta numerical methods, such as Runge-Kutta 2 or 4. As in all models, we start with some initial conditions and parameters. For this model, we will assume a temperature T of 298 Kelvin (0 degrees Celsius is 273 Kelvin, so 298 K
is about 25 degrees Celsius, or about 80 degrees Farenheit, a nice warm day -- but
you already knew how to do that conversion, didn't you!)
We can also look at the algorithms for this model broken down by input and output for each of the three species:
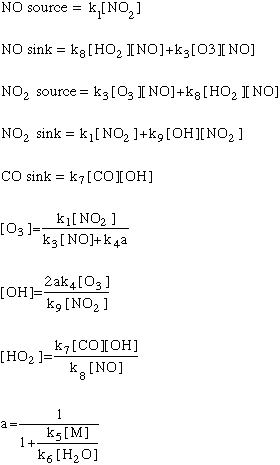
As in all models, we will need some initial conditions:
Initial Conditions (pp
| TRIAL
| 1
| 2
| 3
| 4
|
| [NO2]o
| 10
| 100
| 200
| 1000
|
| [NO]o
| 10
| 500
| 500
| 500
|
| [CO]o
| 50
| 10000
| 10000
| 10000
|
In each case assume that the photolysis rate constant for NO2 (R1 above) is:
kNO2 = 0.533 min-1
Some other helpful info to use:
[H2O] = 0.3x1018 [molecule/cm3]
[M] = 0.2x1020 [molecule/cm3]
k5=2.9x10-11 cm3/molecule-sec
k6=2.2x10-10 cm3/molecule-sec
Conversion factor: 1 molecule/cm3 = 4.08x10-11 parts per billion (ppb)
All of the other k values needed -- k4, k7, k8, and k9 -- can be found on the table
of reactions.
|

