The understanding of cardiovascular function depends on measurements based on a variety of underlying mathematical concepts. The goal of the model is to help users comprehend the mathematical concepts and the important terms defining how the cardiovascular system behaves. The purpose of this interactive simulation is to teach medical students and other users about the complex interactions of the cardiovascular system.
To implement the cardiovascular simulations one must use powerful research computers using high-level languages. A simple model, known as the "Windkessel model" has been developed to allow students to learn about cardiovascular behavior. The computer system presented here achieves this result with a flexible student interface.
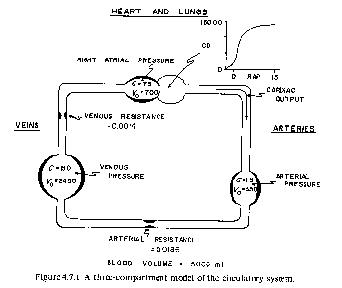
A three-compartment model was designed on the STELLA program and was converted into the perl programming language for installation on a UNIX machine. Its purpose is to provide an easy-to-use model to help you understand how the cardiovascular simulation work. Next, you will be experimenting with various things on the Windkessel model. It requires you to solve several mathematical equations to comprehend the performance of the model. In addition, the components interact in complex ways, and the system exhibits hierarchical organization and multiple time scales.
Three Windkessel compartments--representing the arteries, veins, and right atrium--have been interconnected to complete the circulatory loop. Each compartment is characterized by two variables, pressure and volume, and two parameters, compliance and unstressed volume. Total blood volume is assumed to be 5000 ml.
In the equations that follow, P, F, and V represent pressure (mmHg), flow (ml min-1), and volume (ml), respectively. C is compliance (ml mmHg-1), Vo is unstressed volume (ml), and R is resistance (mmHg min ml-1).

Flow through a blood vessel is determined by two factors: 1) the pressure difference between the two ends of the vessel, called "pressure gradient," which is the force that pushes the blood through the vessel, and 2) the impediment to blood flow through the vessel, which is called vascular resistance.
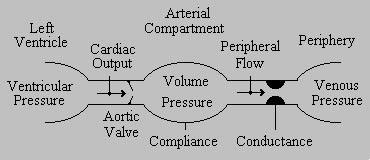
Windkessel consists of four components: left ventricle, aortic valve, arterial vascular compartment, and peripheral flow pathway.
The independent variable is time (t). The units are minutes.
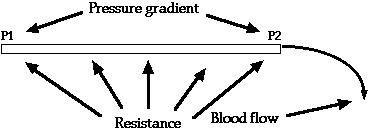
P1 represents the pressure at the origin of the vessel; at the other end the pressure is P2. Resistance to flow occurs as a result of friction all along the inside of the vessel. The flow through the vessel can be calculated by the following formula, which is called Ohm's law:
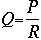
in which Q is blood flow, P is the pressure difference (P1-P2) between the two ends of the vessel, and R is the resistance. This formula states that the blood flow is directly proportional to the pressure difference but inversely proportional to the resistance. That means that the pressure of both ends of the vessel are different and that determines the rate of flow. For instance, if the both ends of the segment were 100 mm Hg pressure and yet no difference existed between the two ends, there would be no flow despite the presence of 100 mm Hg pressure.