Course Chapters
Section Tests
Online Calculators Linear Least Squares Regression Newton's Method Equation Solver
Related Information Links
|
Newton-Raphson MethodIf you've ever tried to find a root of a complicated function algebraically, you may have had some difficulty. Using some basic concepts of calculus, we have ways of numerically evaluating roots of complicated functions. Commonly, we use the Newton-Raphson method. This iterative process follows a set guideline to approximate one root, considering the function, its derivative, and an initial x-value. You may remember from algebra that a root of a function is a zero of the function. This means that at the "root" the function equals zero. We can find these roots of a simple function such as: f(x) = x2-4 simply by setting the function to zero, and solving:
(x+2)(x-2) = 0 x = 2 or x = -2 The Newton-Raphson method uses an iterative process to approach one root of a function. The specific root that the process locates depends on the initial, arbitrarily chosen x-value.
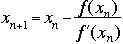
Here, xn is the current known x-value, f(xn) represents the value of the function at xn, and f'(xn) is the derivative (slope) at xn. xn+1 represents the next x-value that you are trying to find. Essentially, f'(x), the derivative represents f(x)/dx (dx = delta-x). Therefore, the term f(x)/f'(x) represents a value of dx.
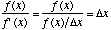
The more iterations that are run, the closer dx will be to zero (0). To see how this works, we will perform the Newton-Raphson method on the function that we investigated earlier, f(x) = x2-4. Below are listed the values that we need to know in order to complete the process.
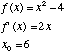
Theoretically, we could execute an infinite number of iterations to find a perfect representation for the root of our function. However, this is a numerical method that we use to lessen the burden of finding the root, so we do not want to do this. Therefore we will assume that the process has worked accurately when our delta-x becomes less than 0.1. This value of precision should be specific to each situation. A much more, or a much less, precise value may be appropriate when using the Newton-Raphson method in class. The table below shows the execution of the process.
A graphical representation can also be very helpful. Below, you see the same function f(x) = x2-4 (shown in blue). The process here is the same as above. In the first iteration, the red line is tangent to the curve at x0. The slope of the tangent is the derivative at the point of tangency, and for the first iteration is equal to 12. Dividing the value of the function at the initial x (f(6)=32) by the slope of the tangent (12), we find that the delta-x is equal to 2.67. Subtracting this from six (6) we find that the new x-value is equal to 3.33. Another way of considering this is to find the root of this tangent line. The new x-value (xn+1) will be equal to the root of the tangent to the function at the current x-value (xn).
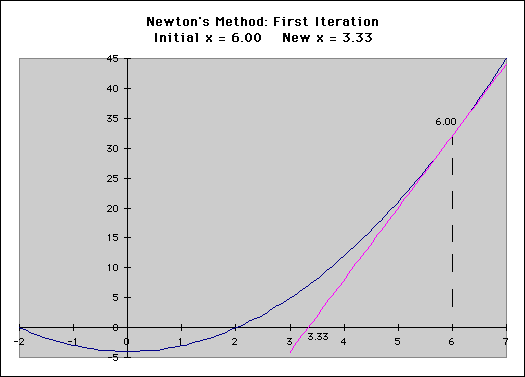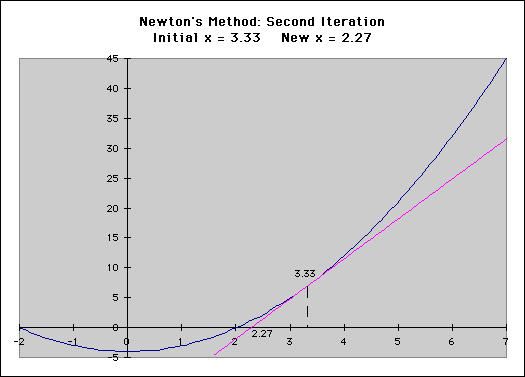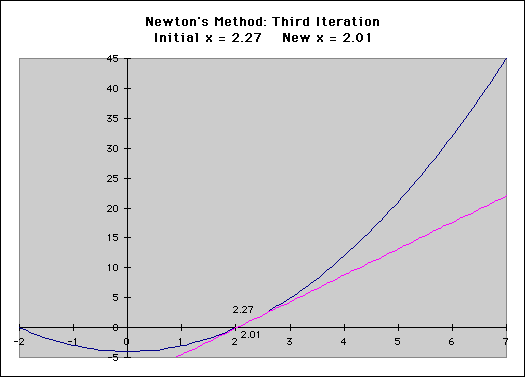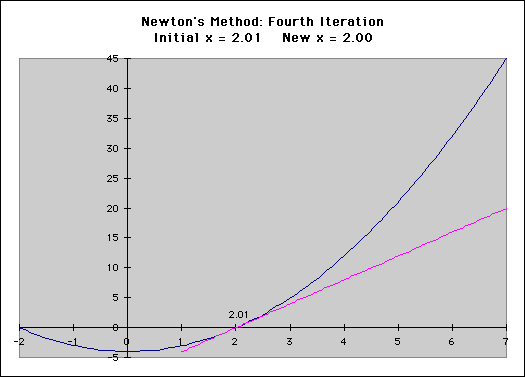
The Newton-Raphson method does not always work, however. It runs into problems in several places. First, consider the above example. What would happen if we chose an initial x-value of x=0? We would have a "division by zero" error, and would not be able to proceed. You may also consider operating the process on the function f(x) = x1/3, using an inital x-value of x=1. Do the x-values converge? Does the delta-x decrease toward zero (0)? So, how does this relate to chemistry? Consider the van der Waals equation found in the Gas Laws section of this text. Assuming that we have a set number of moles of a set gas, not under ideal conditions, we can use the Newton-Raphson method to solve for one of the three variables (temperature, pressure, or volume), based on the other two. To do this, we need to use the van der Waals equation, and the derivative of this equation, both seen below.
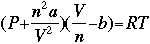
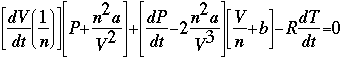
As you can see, the Van der Waals equation is quite complex. It is not possible to solve it algebraically, so a numerical method must be used. The Newton-Raphson Method is the easiest and most dependable way to solve equations like this, even though the equation and its derivative seem quite intimidating. Depending on the conditions under which you are attempting to solve this equation, several of the variables may be changing. So, it may be necessary to use partial derivatives. For the purposes of this example, we are assuming that pressure, temperature, and volume are the only things changing, and that these values are all functions of time. This avoids the use of a partial derivative; we simply differentiate all variables with respect to time, as shown above. Some algebraic manipulation of the equation and/or its derivative may be needed depending on the specific problem to be solved. It is assumed that all of the variables but one are specified; that variable is used in the expression for "xn+1" that Newton's method uses. Performing Newton's method on this equation successfully would give a value of that variable which gives a solution when the other variables are held constant at the values you specified. Newton's Method Equation Solver: An Online Interactive Tool
|
 Shodor
Shodorin cooperation with the Department of Chemistry,
The University of North Carolina at Chapel Hill
Copyright © 1996-2008 Shodor
Please direct questions and comments about this page to
WebMaster@shodor.org