Course Chapters
Section Tests
Online Calculators Linear Least Squares Regression Newton's Method Equation Solver
Related Information Links
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Answer: | ||||||||||||||||||||||||||||
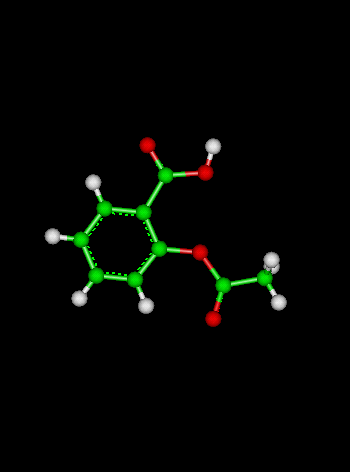
| we must first convert our values to molarity: | ||||||||||||||||||||||||||||
3 L |
= 2 M | |||||||||||||||||||||||||||
| fill in the "start, change, equilibrium" chart: | ||||||||||||||||||||||||||||
| C2H6 (g) | + | Cl2 (g) | → | C2H2Cl (s) | + | HCl (g) | ||||||||||||||||||||||
| Start: | 2 M | 2 M | -- | 0 M | ||||||||||||||||||||||||
| Change: | - x | - x | -- | + x | ||||||||||||||||||||||||
| Equilibrium: | 2 - x | 2 - x | -- | x | ||||||||||||||||||||||||
| now substitute what we know into the equilibrium constant expression and solve for x: |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
| .40 - .40x + .1x2 = x | ||||||||||||||||||||||||||||
| .10x2 - 1.4x + .4 = 0 | ||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
| PCl2 = .4167 atm | ||||||||||||||||||||||||||||
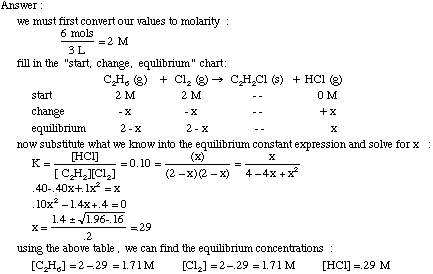
Le Chatelier's principle allows us to predict the effects of changes in temperature, pressure, and concentration on a system at equilibrium. It states that if a system at equilibrium experiences a change, the system will shift its equilibrium to try to compensate for the change.
- changing the concentration (only with gases or aqueous solutions):
If you lower the concentration or remove some of a species, the system will shift to produce more of that species. On the other hand, if you increase the concentration or add some of a species, the system will shift to produce less of that species. For example, in the equation:H2+ I2 <--->2HI If we remove some of the H2, the system will shift towards the left (the reverse reaction will happen the most) to produce more H2.
- changing the volume/pressure (only gases):
Increasing the volume has the same effect as decreasing the pressure and vice versa so we are only going to talk about changing the pressure. When you increase the pressure, the system will shift so the least number of gas molecules are formed because the more gas molecules there are, the more collisions there are. These collisions and the presence of gas molecules are what cause the pressure to increase. Likewise, when you decrease the pressure, the system will shift so the highest number of gas molecules are produced. For example, in the equation:N2 (g) + 3H2 (g) <---> 2NH3 (g)
if the pressure is increased, the system will shift to the right because fewer gas molecules are produced in the forward reaction than in the reverse reaction. - changing temperature:
For every reaction which can go forwards and backwards, one direction is endothermic and the other is exothermic. A reaction is endothermic if it takes heat from its surroundings. On the other hand, a reaction is exothermic if it gives heat to the surroundings. If you increase the temperature, then the endothermic reaction will be favored because that will take in some of the excess heat. If you decrease the temperature, the exothermic reaction will be favored because it will produce the heat that was lost. For example, in the equation:PCl3(g) + Cl2(g) <----> PCl5(g) + energy if the temperature was increased, the system would shift to the left and the reverse reaction would happen more because that would use some of the extra energy.
- using a catalyst:
A catalyst increases the speed in which a reaction takes place, however it never has any effect on the equilibrium.
Ksp=[Ag+][Br-]
Adding common ions, acids, or bases affects the solubility of a substance. Taking the above reaction as an example, if you add AgNO3, the [Ag+] would increase causing the system to shift to the left and therefore causing the solubility to decrease. If you add Pb(NO3)2, the Pb2+ and the Br- would form a precipitate which would decrease the [Br-] and cause the system to shift to the right and therefore increase the solubility. Look at the following reaction:
If you add HNO3, the weak acid HF would form which will lower the F- concentration and cause the system to shift to the right and therefore increase the solubility. You should watch out for the formation of a precipitate or the formation of a weak acid when dealing with solubility reactions.
Example Ksp Problem:
0.100 L of 0.003 M Pb(NO3)2 is added to 0.400 L of 0.005 M Na2SO4. Will PbSO4 precipitate? Ksp=1.6x10-8
Practice Equilibrium Problem:
At a certain temperature, a 1.00L flask initially contained 0.298 mol PCl3(g) and 0.00870 mol PCl5(g). After reaching equilibrium, 0.00200 mol Cl2(g) was found in the flask. PCl5 decomposes according to the equation:
Calculate the equilibrium concentrations of the three molecules and the value of K.
equilibrium solution.
Practice Ksp Problem:
Ksp for SrSO4=7.6x10-7. Ksp for SrF2 =7.9x10-10.
a) What is the molar solubility of SrSO4 in pure water?
b) What is the molar solubility of SrF2 in pure water?
c) Sr(NO3)2(aq) is added to 1.0 L of solution containing 0.020 mol F- and 0.10 mol SO42- with constant volume. 1: which salt precipitates first? 2: What is [Sr2+] in solution when precipitate forms?
Ksp solution.
[Advanced Index]
[Gas Laws]
[Thermodynamics]
[Kinetics]
[Equilibria]
[Redox Reactions]
[Nuclear Chemistry]
 Shodor
Shodorin cooperation with the Department of Chemistry,
The University of North Carolina at Chapel Hill
Copyright © 1996-2008 Shodor
Please direct questions and comments about this page to
WebMaster@shodor.org