| (28) |
Because our building's stiffness-mass-damper system has more than one mass, the solution of the
equation (28) requires solving det
![]() = 0
for
= 0
for ![]() .
Substituting the mass, damping, and stiffness matrices into this determinant equation, we get a sixth degree polynomial.
Unfortunately, unlike the single degree of freedom system, there is no way to solve the determinant equation for
.
Substituting the mass, damping, and stiffness matrices into this determinant equation, we get a sixth degree polynomial.
Unfortunately, unlike the single degree of freedom system, there is no way to solve the determinant equation for ![]() in terms of
in terms of ![]() ,
,
![]() , and
, and ![]() .
Luckily, though, if numerical values exist for
.
Luckily, though, if numerical values exist for ![]() ,
, ![]() , and
, and ![]() ,
they can be used to solve the equation instead.
,
they can be used to solve the equation instead.
When dealing with the physical model, we do have numerical values.
Because the building is under-damped, be have three complex-conjugate pairs of values for ![]() .
.
Furthermore, since the damping matrix is of the form ![]() (ie., damping is stiffness and mass proportional), it can be shown that
the natural frequencies of a multi-mass system are independent of damping.
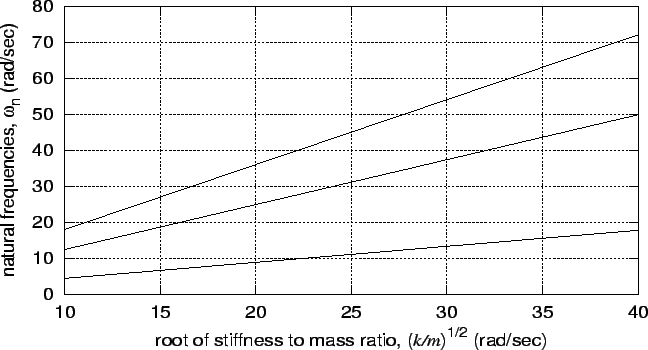
In Figure 6 below, the three natural frequencies,
(ie., damping is stiffness and mass proportional), it can be shown that
the natural frequencies of a multi-mass system are independent of damping.
In Figure 6 below, the three natural frequencies,
![]() ,
,
![]() , and
, and
![]() are plotted with respect to the
square root of the ratio of the story shear stiffness,
are plotted with respect to the
square root of the ratio of the story shear stiffness, ![]() , to the floor mass
, to the floor mass ![]() ,
, ![]() .
The natural frequencies for this structure are approximately
.
The natural frequencies for this structure are approximately
![]() ,
,
![]() , and
, and
![]() .
.
 |
| You can use the frequency calculator at right to input different values of mass, stiffness, and damping and find out what the model building's natural frequencies would be in that case. You can see that changing the damping doesn't affect the natural frequencies, just the damped natural frequencies. Also, note the relationships graphed in Figure 6 can be determined from this calculator. What other concepts from this section can be illustrated with this calculator? |
|
With knowledge of natural frequencies and damping ratios, we may now numerically determine the constants
![]() .
This may be done by substituting
.
This may be done by substituting
![]() and
and ![]() into equation (27)
and then substituting
into equation (27)
and then substituting ![]() into equation (28) and solving for
into equation (28) and solving for ![]() .
For every natural frequency
.
For every natural frequency
![]() and damping ratio
and damping ratio ![]() ,
, ![]() , the vector
, the vector ![]() is zero.
The fact that the vectors
is zero.
The fact that the vectors ![]() are real in this problem is another desirable property of proportionally damped systems.
With the simplification that the vectors
are real in this problem is another desirable property of proportionally damped systems.
With the simplification that the vectors ![]() are real, the solutions become
are real, the solutions become
In general, we will assume that the free displacement response of our three-story building
is made up of the sum of three distinct damped oscillations, each with a different frequency ![]() and damping
and damping ![]() ,
,
![]() .
This trial solution can be written as
.
This trial solution can be written as
![]() ,
where the three-by-three modal matrix
,
where the three-by-three modal matrix ![]() is a column-wise combination of the vectors
is a column-wise combination of the vectors ![]() ,
, ![]() and
and ![]() .
If the initial condition
.
If the initial condition ![]() is only in a single mode, then the free response will remain entirely in that mode.
is only in a single mode, then the free response will remain entirely in that mode.