Finding the Moon's greatest and least speeds
This page provides the teacher with questions and answers to help guide the class through the exercise of finding the speed of the Moon.
Background:
Ask the students to explain how each of the three scientists changed our thoughts about planetary motion.
Area of the ellipse:
|
Area of an ellipse = pi * a * b pi = 3.141 in a spreadsheet pi =pi() Area of a triangle = 1/2* base* height a = 1/2 the major axis b = 1/2 the minor axis |
|
closest perigee = 359861 km farthest apogee = 405948km Time for one orbit of the Earth = 27.32166 days The sun tugs on the moon. This distorts the moon's orbit. About once each year the moons apogee points toward the sun. This makes the apogee larger than at other times. |
Area of an ellipse = pi * a * b
You need to find pi, a and b. Then substitute them into the equation.
a = 1/2 the length of the major axis.
The diagrams show you how to find the length of the major axis.
major axis = apogee + perigee
major axis =(405948km +359861km)
a = (apogee + perigee)/2
382904.5km
To find b you need to remember how we drew the ellipse. You will also need to construct a triangle.
The corners of the triangle are:
a foci, the intersection of the major and minor axis, and the intersection of b and the ellipse.
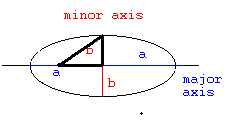
How can you find the length of the line segment from the foci to the intersection of a, b?
Think about perigee and 1/2 the major axis.
Line segment = a - perigee
Line segment = 382904.5km -359861 km
Line segment = 23043.5km
How can you find the length from the foci to the intersection of b and the ellipse?
Think about the string we used to draw the ellipse.
First calculate the total length of the string.
length of string = 2 * apogee, When the string runs from a focus along the major axis to the point on the major axis both sides of the string touch. This is the apogee. Since the string covers this distance two times its length is
2 * the apogee.
811896km
Second subtract the length of string that connects the foci.
The distance between the foci is the apogee - perigee.
2*apogee-(apogee - perigee)=
811896km-(46087km)
or
2*apogee - apogee + perigee=
apogee + perigee
405948km+359861km
765809km
Now you have the length from a foci to the ellipse and back to the other foci.
From this you can find the length from the foci to the ellipse.
(apogee + perigee)/2
382904.5
Use the Pythagorean theorem to find the length of the line b.
((apogee+perigee)/2)^2 = ((apogee + perigee)/2)^2 + b^2
((apogee+perigee)/2)^2 - ((apogee + perigee)/2)^2 = b^2
(((apogee+perigee)/2)^2 - ((apogee + perigee)/2)^2)^1/2 = b
^2 means squared
^1/2 means find the square root of
b=382210.5km
Now you know a and b and pi.
Substitute them into the equation above and you will find the area of the orbit of the moon.
Hint: When the students construct their spreadsheet, they should make cells devoted to each of these calculations. When a calculation needs value that has already been calculated simply refer to the cell that contains that value. i.e. if we calculate a in cell B3 and we calculate b in D5 then
Area of an ellipse = pi * B3 * D5
4.59772E+11km^2= 459,772,000,000 km^2
Your answer will vary depending on the value you use for pi. Different calculators and spreadsheets have different built in values for pi. It is important for students to understand that the tools we use effect the answers we get. It isn't that one is right and another is wrong. In science, unlike math, all measurements and numbers have some error or uncertainty. We need to take that into consideration when we think about our answer.
Remember: Law 2; A line joining a planet/comet and the Sun sweeps out equal areas in equal intervals of time.
This means that each hour the area swept out is the same.
You know the total area. You know the number of hours it takes the Moon to go around the Earth.
You can calculate the area swept out each hour.
Lunar cycle = 27.32166 days
Lunar cycle = 27.32166days * 24hour/day
Lunar cycle = 655.71984hours
Area / hour = 459,772,000,000 km^2/655.71984hours
701172077.6km^2/hr
Now you can find the speed for these hourly movements.
You need to remember the area of a triangle. Area = 1/2 the base * the height.
The height is the distance from the earth to the moon.
The base is the part of the ellipse that the moon traverses. For our purposes we will assume that that is a straight line.
You know the area.
Use the area and the height to find the base.
Area = 1/2 base * height
2*Area/height= base
2*701172077.6km^2/hr/apogee km=
3454.5km/hr at apogee
2*701172077.6km^2/hr/perigee km=
3896.9km/hr at perigee
Since the base was traversed in one hour it is the distance the moon travels per hour or the speed per hour.
Do this calculation for the shortest (perigee) and longest (apogee) heights.
You now have the Moon's fastest and slowest speeds.
Ask the students to compare these speeds.
The difference is 442.4 km/hr
Ask the students to calculate the average speed of the moon.
Average speed = 3675.7km/hr
Ask the students to compare the difference in speed with the average speed.
The difference is 12% of the average speed.
The speed at apogee is only 88.6% of the speed at perigee.
Now transfer these calculations to a spreadsheet.
Use a cell to input the apogee.
Use a cell to input the perigee.
Use a cell for the period of revolution in hours.
Use cells for each of the above calculations.
This spreadsheet will help you calculate the range of speeds for all of the planets.
If you look on the internet you can find perigee, apogee and orbital period for several comets and asteroids.
http://cfa-www.harvard.edu/mpec/K02/K02R06.html
http://cfa-www.harvard.edu/cfa/ps/lists/Atens.html
http://cfa-www.harvard.edu/iau/Ephemerides/Comets/index.html
On these tables q is perihelion or perigee (AU), Q is aphelion
or apogee (AU), P is the period in years, e is the eccentricity, a is the semi major
axis( half the major axis.)
Your nifty spreadsheet will find the range of speeds for all of these objects!
You may find it useful to open the student version of:
in a separate window. This will allow you to toggle between the teacher discussions and the student lesson.


