In Measure to Measure we will build open boxes out of a paper grid
in an attempt to optimize, or make as perfect as possible, the surface
area and the volume of the box.

Let's look at the piece of grid paper. Find the area by multiplying the number of boxes on one side by the number of boxes on the other side. For this grid, the dimensions are 19 x 25, which equals 475. But 475 what? In science we should describe our measurement in units so that other scientists understand what we are measuring. If we were using a standard measurement, like centimeters or inches, we should record those values. In this case, however, we only care that our grid is made of equally sized units of area that are the same width and length, i.e. that they are square. Our grid paper (not including the borders) has an area of 475 square units.
Let's turn this two-dimensional area into a three-dimensional box.
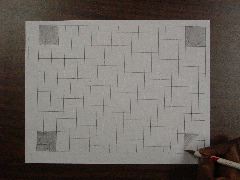
Print out the grid paper onto a heavy piece of
card-stock paper. Shade in a 3x3 square (or, if working as part of a class,
use one of other options for square corner cuts as listed on page 3) on each corner of your piece of paper grid.
We'll call this a "cut" of 3 (since these corners will be cut so as not to be
part of the box). You may cut these squares out, but it
is easier to tape them together if you cut tabs.
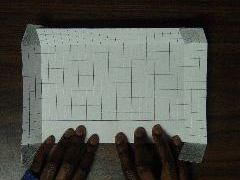
To do this, cut only from the longer side (the 25 unit side). Then, tape
the sides together to form an open box.
4 steps to a box!
 1. draw squares |
 2. cut tabs |
 3. fold edges |
 4. tape together |
For a cut of 9, the tab is too long. To fix this problem, cut the tab to make it shorter, as indicated in the picture below.

Now let's consider some measurements of the box we have created.
| On to Page 2! |