Bounce
Lesson - Bounce (Projectile motion and collisions)Gravity is a force which causes any mass to attract any other mass. On the surface of the Earth, the largest object nearby is the earth itself, and all objects on the Earth's surface are held onto the Earth by the Earth's gravitational pull. While the gravitational force on any two masses near the surface of the Earth does not need to be the same (and is in fact larger for larger masses), the acceleration caused by that force is the same for all objects near the Earth's surface, even if we are considering a bowling ball and a BB. The force on any object near the Earth's surface due to the Earth is given by F=mg, where g is the acceleration due to gravity. At sea level, this acceleration is approximately 9.8 m/s2. To consider the action of gravity on an object, consider a ball which rolls off of a table and bounces on the floor. The ball in the bounce experiment will undergo primarily three phases: resting on a table, free fall, and bouncing. The fundamental forces during each of these phases are:
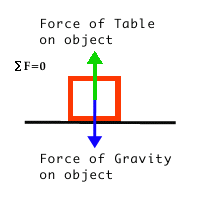
Resting on Table:While the object is resting on the table, it does not move up or down, that is, it's velocity in the y direction is zero the entire time. If the velocity is not changing, then it's acceleration is also zero. By Newton's Second Law, we see that if the acceleration of the object is zero, the net force on the object is also zero.
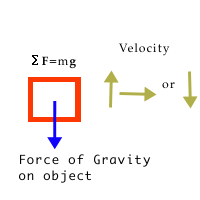
Free Fall:When the object is in free fall, only gravity acts on the object (neglecting air resistance).
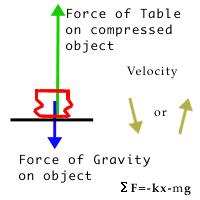
Bouncing:When the object bounces, it compresses as it hits the table. Assuming the table does not compress, the force given by the compression is equal to the spring constant of the object times the compression, and is in the direction opposite the compression, F=-kx. In the case of the ball falling on the table, the table presses back against the ball in an upwards direction. This is similar to the normal force, except that the compression of the ball results in a force greater than the weight of the ball, and it is propelled upwards.
Using data from the web or from an experiment of your own construction, measure the position of a ball at differnt times as it rolls off a table and onto the floor. Calculate the first and seconf derivative of the position and answer the following questions. Questions:
Advanced Questions:
|