Energy Balance Model: Application and Background

Mathematically, we can describe the energy balance model as follows:

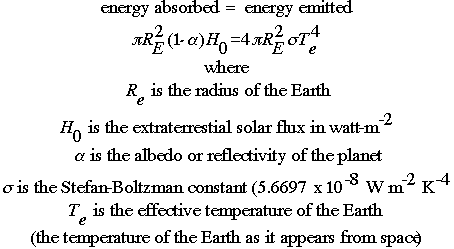
Energy balance models are typically one-dimensional, that dimension being latitude. What we are trying to calculate is the temperature at the surface. The model itself aims to calculate the effective temperature, T_e. We are interested in the temperature at the surface, or T_s. The following calculation is used to calculate T_s:

where dT is the greenhouse increment. At this time, the greenhouse increment is about 33 degrees Kelvin, and is a function of the efficiency of the infrared absorption.

All this would be fairly simple except for the fact that most energy balance models are not global models, but zonal, or latitudinal, models. As such, we must have some equation or part of an equation that accounts for the flow of energy from one latitudinal zone to the next. The graphic below shows a zonal one-dimensional energy balance model:

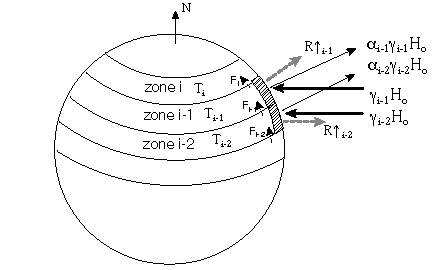
In this schematic, we are showing that the equation has now become:

In this model, the incoming energy due to the sun must be adjusted to account for the spherical shape and orbital variations of the Earth. Each zone can, and usually does, have its own albedo, or reflectivity. Each zone also has its own zonal surface temperature which usually includes the greenhouse increment.

In the zonal model, we need to be able to calculate the total energy received from the sun per unit time. This is given by:

R²H₀

where R is the radius of the Earth and H₀ is the solar constant. Given that the Earth's total area can be calculated by 4R², we can propose the equation:

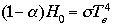
where, as before, 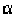is the planetary albedo, H₀ is the solar constant, and is the Stefan-Boltzmann constant. The average extraterrestrial solar flux over the entire surface can by calculated by H₀/4.

We also need to consider the fact that not all zones receive the same amount of incoming radiation, since the incident angle of the sun to a particular zone varies. There exists some ratio, 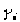, that corrects the average incoming radiation for a given zone. We can then calculate the incoming solar radiation for a given zone as:

incoming radiation = 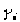H₀/4

We are also concerned with the surface albedo of each zone. These are dependent upon the ratio between land and water and the type of land covering. There exists a critical temperature, T_c, which is that temperature below which the land becomes ice covered. The typical literature value for this temperature is -10.0 degrees C. For a given zone, the surface albedo depends on the surface temperature of that zone. If the surface temperature is below the critical temperature, the albedo for the zone is the albedo of ice, or 0.68. For temperatures above the critical temperature, several equations are used. The most typical is:

Cloud albedo is typically specified as being 0.5. Fractional cloud cover values are a typical input for a standard energy balance model.

The transport of energy between zones is given by:

where:

• C is a constant equal to 3.80 watt-m^-2 C^-1
• T_i is the average temperature of the zone
• T_s is the mean global surface temperature

Again, the purpose of the energy balance model is to calculate the temperature of the zone. A final equation for calculating temperatures is as follows:

This equation is iterated until an equilibrium value is reached, determined by some user-defined tolerance value.

In this model, the incoming and outgoing energy for the individual "zones" are calculated, and the individual temperatures and global mean temperature are calculated.