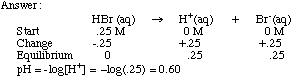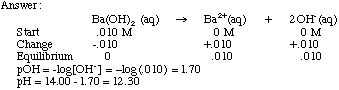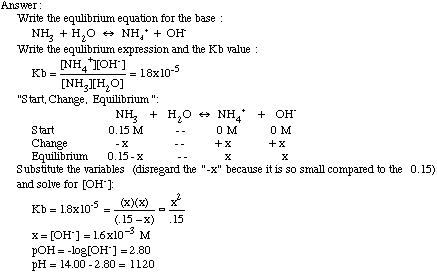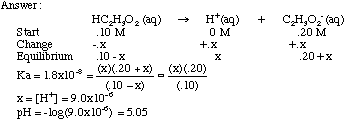
Course Chapters Advanced Concepts
Section Tests
Online Calculators Linear Least Squares Regression Newton's Method Equation Solver
Related Information Links
|
Acid-Base ChemistryWaterWe typically talk about acid-base reactions in aqueous-phase environments -- that is, in the presence of water. The most fundamental acid-base reaction is the dissociation of water:
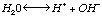
In this reaction, water breaks apart to form a hydrogen ion (H+) and a hydroxyl ion (OH-). In pure water, we can define a special equilibrium constant (Kw) as follows:
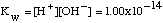
Where Kw is the equilibrium constant for water (unitless) An equilibrium constant less than one (1) suggests that the reaction prefers to stay on the side of the reactants -- in this case, water likes to stay as water. Because water hardly ionizes, it is a very poor conductor of electricity.
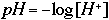
At equilibrium, the concentration of H+ is 10-7, so we can calculate the pH of water at equilbrium as:
Solutions with a pH of seven (7) are said to be neutral, while those with pH values below seven (7) are defined as acidic and those above pH of seven (7) as being basic. pOH gives us another way to measure the acidity of a solution. It is just the opposite of pH. A high pOH means the solution is acidic while a low pOH means the solution is basic.
pH + pOH = 14.00
SaltsA salt is formed when an acid and a base are mixed and the acid releases H+ ions while the base releases OH- ions. This process is called hydrolysis. The pH of the salt depends on the strengths of the original acids and bases:
This is because the conjugate base of a strong acid is very weak and cannot undergo hydrolysis.
Similarily, the conjugate acid of a strong base is very weak and likewise does not undergo hydrolysis.
Strong Acids: These acids completely ionize in solution so they are always represented in chemical equations in their ionized form. There are only seven (7) strong acids:
To calculate a pH value, it is easiest to follow the standard "Start, Change, Equilibrium" process.
Example Problem: Determine the pH of a 0.25 M solution of HBr. Weak Acids: These are the most common type of acids. They follow the equation:
The equilibrium constant for the dissociation of an acid is known as Ka. The larger the value of Ka, the stronger the acid.
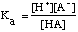
Example Problem: Determine the pH of .30 M acetic acid (HC2H3O2) with the Ka of 1.8x10-5. Strong Bases: Like strong acids, these bases completely ionize in solution and are always represented in their ionized form in chemical equations. There are only seven (7) strong bases:
Example Problem: Determine the pH of a 0.010 M solution of Ba(OH)2. Weak Bases: They follow the equation:
example: NH3 + H2O <---> NH4+ + OH+ Kb is the base-dissociation constant:
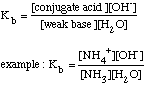 Ka x Kb = Kw = 1.00x10-14 To calculate the pH of a weak base, we must follow a very similar "Start, Change, Equilibrium" process as we did with the weak acid, however we must add a few steps.
Example Problem: Determine the pH of 0.15 M ammonia (NH3) with a Kb=1.8x10-5. When dealing with weak acids and weak bases, you also might have to deal with the "common ion effect". This is when you add a salt to a weak acid or base which contains one of the ions present in the acid or base. To be able to use the same process to solve for pH when this occurs, all you need to change are your "start" numbers. Add the molarity of the ion which comes from the salt and then solve the Ka or Kb equation as you did earlier.
Example Problem: Find the pH of a solution formed by dissolving 0.100 mol
of HC2H3O2 with a Ka of
1.8x10-8 and 0.200 mol of NaC23O2 in a total volume of 1.00 L.
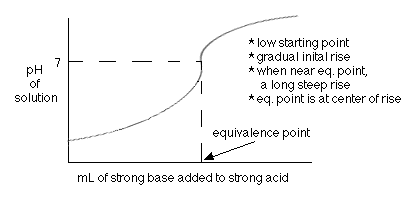 For the titration of a strong base with a weak acid, the equivalence point is reached when the pH is greater than seven (7). The half equivalence point is when half of the total amount of base needed to neutralize the acid has been added. It is at this point where the pH = pKa of the weak acid.
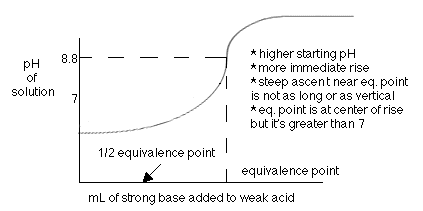 In an acid-base titration, the base will react with the weak acid and form a solution that contains the weak acid and its conjugate base until the acid is completely gone. To solve these types of problems, we will use the weak acid's Ka value and the molarities in a similar way as we have before. Before demonstrating this way, let us first examine a short cut, called the Henderson-Hasselbalch Equation. This can only be used when you have some acid and some conjugate base in your solution. If you only have acid, then you must do a pure Ka problem and if you only have base (like when the titration is complete) then you must do a Kb problem.
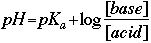 Where: Example Problem: 25.0 mL of .400 M KOH is added to 100. mL of .150 M benzoic acid, HC7H5O2 (Ka=6.3x10-5). Determine the pH of the solution.
This equation is used frequently when trying to find the pH of buffer solutions. A buffer solution is one which resists changes in pH upon the addition of small amounts of an acid or a base. They are made up of a conjugate acid-base pair such as
HC2H3O2/C2H3O2- or NH4+/NH3. They work because the acidic species neutralize the OH- ions while the basic species neutralize the H
Practice weak acid problem:
C6H5COONa is a salt of a weak acid C6H5COOH. A .10 M solution of C6H5COONa has a pH of 8.60.
See the weak acid solution.
Practice titration problem:
20.00 mL of
0.160 M HC2H3O2 (Ka=1.8x10-5) is titrated with .200 M NaOH.
See the titration solution.
[Basic Index]
[Atomic Structure]
[Stoichiometry]
[Acid Base Chemistry]
[Nomenclature] |
 The Shodor Education Foundation, Inc.
The Shodor Education Foundation, Inc.in cooperation with the Department of Chemistry,
Appalachian State University
Copyright © 1998
Last Update:
Please direct questions and comments about this page to
WebMaster@shodor.org