CASE STUDY: Influenza Epidemic in a Boarding School

Source: Mathematical Biology, J.D. Murray, Springer-Verlag, 1989.

Background:

In 1978, a study was conducted and reported in the British Medical Journal (4 March 1978) of an outbreak of the influenza virus in a boys boarding school. The school had a population of 763 boys. Of these 512 were confined to bed during the epidemic, which lasted from 22 January until 4 February. It seems that one infected boy initiated the epidemic. At the outbreak of the epidemic, none of the boys had previously had influenza, so no resistance to the infection was present.

Modeling Task:

Build a computational model of this epidemic, looking to answer these two questions:

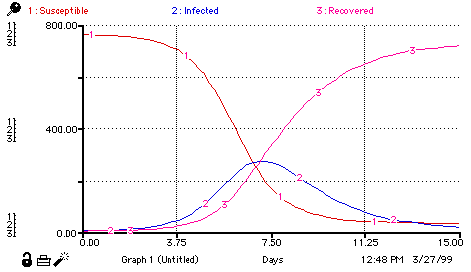
1. On what day (with Day 0 being the beginning of the epidemic) did the majority of the boys have the flu?

2. At what time did most or all of the boys recover from the illness?

To build this model, you should use the 1927 Kermack-McKendrick model known as the SIR algorithm. This algorithm looks at the change in three populations: susceptibles (S), infecteds (I), and recovereds (R). It assumes that once recovered, immunity from recontamination exists and therefore a patient cannot re-enter the susceptible or infected group. The algorithm is shown below in differential equation form:

dS/dt = -rSI

dI/dt = rSI - aI

dR/dt = aI

where S is the total susceptible population, I is the total infected population, R is the total recovered population, r is the infection rate and a is the removal rate of infectives (the recovery rate). We are, of course, only interested in non-negative solutions for S, I, and R. This is a very primitive algorithm, but provides relatively good results, especially in looking for the epidemic "hump". This algorithm assumes a constant population, that is, no immigration or emigration of potential players. This also assumes, naturally, that no one dies of the illness! In this model 1/a is the average infectious period. In this model, the infection rate is about 0.00218 per day, and the removal rate is approximately 1/2 per day -- an average infectious period of about two days.

Once you have built your model, show the three populations on your graph. You might also consider using a "Total Population" converter to ensure that all 763 boys are accounted for at all times.

Extension:

What would happen if some of the boys had been vaccinated prior to the beginning of the epidemic? Let's assume that 10% of the susceptible boys are vaccinated each day -- some of them getting the shot while the epidemic is happening in order not to get sick (this assumes, falsely, that instant immunity is realized once you've received the shot). Experiment with the 10% vaccination rate to determine how it changes the intensity and duration of the epidemic.
The completed model should look like this:



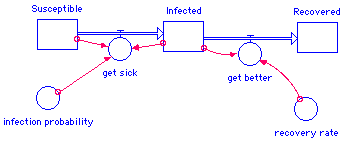
Equations are:

Infected(t) = Infected(t - dt) + (get_sick - get_better) * dt
INIT Infected = 1

INFLOWS:
get_sick = infection_probability*Susceptible*Infected
OUTFLOWS:
get_better = recovery_rate*Infected
Recovered(t) = Recovered(t - dt) + (get_better) * dt
INIT Recovered = 0

INFLOWS:
get_better = recovery_rate*Infected
Susceptible(t) = Susceptible(t - dt) + (- get_sick) * dt
INIT Susceptible = 762

OUTFLOWS:
get_sick = infection_probability*Susceptible*Infected
infection_probability = 0.00218
recovery_rate = 1/2

Results graph: