



|
|
|
For thousands of years, philosophers have considered the initial act of the speculative intellect to be the realization that a statement,together with its direct negation, cannot both be true at the same time. This so-called principle of non-contradiction, or what Aristotle called the first principle of demonstration, is an essential operating rule for human reason. It can be found in various forms in literature ("To be, or not to be, that is the question"), common adages ("You can't have your cake and eat it, too"), and parental frustration ("What do you mean it's 'sort of' done? Either your homework is finished, or it isn't, so which is it?"). It is also very important in science and mathematics, where we are frequently confronted with an apparent contradiction or paradox that begs for resolution: the human intellect and psyche seem to have a natural aversion to ambiguity and uncertainty. As a result, it has often been said that the battle cry of scientific discovery is not "Eureka!" but rather, "Hmmm, that doesn't look right. So, how can that be?" Many times a paradox results from incomplete or erroneous data. Another possibility is that our understanding of what we observe may be flawed and in need of revision. In fact, radical changes in scientific thought are made much more frequently than commonly believed. At the same time, scientists who insist on holding on to old or comfortable views will miss the opportunity for new discovery and understanding. Consider the case of Galileo, whose struggles to develop his own views of the motions of the earth, the planets and the sun –even when confronted with directly contradictory evidence - have taken on mythical proportions. Part of his problem was that, while he was proposing some new ideas which made others uncomfortable, he was uncomfortable giving some ideas that were common for his age, but which clouded his thinking, such as celestial objects needing to move in perfect, circular orbits, or that the stars are close to the earth. You have to look pretty hard in history-of-science books to realize that none of the major propositions that Galileo held to be "incontrovertible" in his day is believed by anyone in our day. Among the theories that Galileo thought he had proved: that tides are caused by "sloshing" (they are caused by the gravitational pull of the sun and moon), that the earth and all planets revolve around the sun in perfectly circular orbits, or circles upon circles (the orbits are elliptical), that forces are proportional to velocity (they are proportional to changes in velocity), that the sun stands still (it moves), and that his solar system theory as formulated gave better predictions than others of his time (it didn't). Let's consider one paradox from that age and consider how significant advances in both technology and attitude enabled science to advance. About 400 years ago, a test was conducted to see if Galileo's assertion that the earth was moving was true: they searched for parallax. Parallax is the apparent movement that close objects make against a more distant background when the point of reference is changed. To observe parallax yourself, try the following: close one eye, and holding your arm out, using your thumb as a "sight". Line up some distant object with your thumb. Now, without moving your arm, switch which eye is open and which is closed. The apparent movement that you perceive is a result of parallax. Now consider this in the context of what was believed by everyone at the time of Galileo, including Galileo. They believed that all stars were identical, and that the brighter ones were merely closer than the dimmer ones, and that all stars were relatively close to the earth. So if the earth moved, as Galileo proposed, over the course of six months, then the brighter stars would appear to shift against the background of dimmer stars, as the line of sight from the earth shifted, as in the diagram below. |
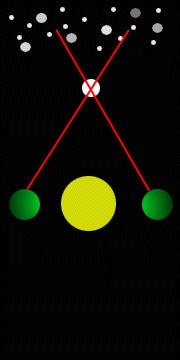
|
|
Was any parallax observed? None, whatsoever! Then, did that mean that the earth wasn't moving? How could the earth both move (theory) and not move (observation) at the same time and in the same way? The resolution of this parallax paradox did not come for hundreds of years, after the invention of photographic plates and the willingness to give up the ideas that the only determination of brightness for a star was its distance and that the stars are close. With very long exposures of photographic plates, there is a measurable parallax, but the effect was very much smaller than Galileo or others thought it would be, because the stars are so very much farther away than anyone ever thought they could be.
Other paradoxes that come to us from astronomical observations have to do with how one analyzes light from distant stars. The study of light across the color spectrum, called spectroscopy, is an important tool for determining the chemical composition and even temperature of stars and other burning objects. When heated, different elements and compositions give off light of different colors. This is because of their characteristic energy shifts: when heated, electrons are promoted into excited levels, different for each kind of material, and then fall back. The energy difference is emitted in the form of a photon of a very specific frequency, or wavelength. When passed through a spectral analyzer, like a prism, light of different frequencies is bent differently, and the various color components are separated and show up as distinct spectral lines. Just as sound appears shifted to higher or lower frequencies depending on whether the source of sound is moving toward or away from you, known as a Doppler shift, if the light source is moving, the locations of the expected spectral lines are shifted. Line shift towards the blue part of the spectrum if the light source is moving towards the observer, and towards the red part of the spectrum if the light source is moving away. This gives rise, for instance, to the "red shift" measurement of the speed with which distant galaxies are appearing to move away from us: the more towards the red part of the spectrum a line is shifted, the faster the source is moving away. If passed through a spectral analyzer in an earth-based laboratory, light from burning sodium exhibits a very "clean" pair of double lines. This same pair of lines can be observed in the spectral lines from many distant stars, but they appear very broad and fuzzy, as if the lines have been shifted both to the blue and red parts of the spectrum! How can this be? In what way(s) can a star be moving both towards us and away from us at the same time? Actually, there are lots of ways, though it has taken some time to unravel them. For instance, suppose the star was rotating. Couldn't that explain part of this double shift, since part of the star could be moving toward you while the other part is moving away, at the same time? The key is to not hold on to the idea that a star is a "point object," even though it appears that way in a telescope. In fact, a star is a very extended object. Another possibility is that the star is turbulent, with large amounts of matter being circulated between the outer parts of the star and its inner core. The parts of the star moving outward would be moving towards us, while the parts of the star moving towards its own core would be moving away from us. Can you think of other reasons? Another paradox is only beginning to be resolved, and that requires extensive reworking of our models of how stars burn. Most current theories of stellar dynamics put the age of some stars at 12 to 18 billion years old, while the new results from the Hubble Space Telescope suggest that the universe may be younger than 12 billion years old. Now, how can that be? Surely, a star cannot both be older than (pre-dating) and younger than (existing in) universe that contains it, can it? The problem has to do with the quality of the models used in cosmology, the study of the cosmos and everything in it. The paradox is beginning to be resolved as more sophisticated models of stars, are suggesting that stars may not be so old as we thought, after all. If true, this would bring estimates of ages of stars and the age of the universe closer together. These newer models require scientists to rethink whether stars are stable structures with well defined layers, as the older models held, or whether there is significant mixing between layers. These newer models require many more calculations than before, with some of these calculations so complicated that they have taken several years on the fastest supercomputers in the world. Much more work is yet to be done by teams of scientists and mathematicians in this country and around the world. In science, the path to resolution for most paradoxes is a change in our assumptions, or an improvement or refinement in our theories. Sometimes we just need better data (observations) on which to base those theories, which may require better technology to achieve. Mathematics is also full of things that seem paradoxical or contradictory. Some apparent paradoxes melt away when we examine our statement of the problem more closely--others remain stubbornly in place, requiring us to rethink the way we look at the (mathematical) world. It is easy to set up an apparent paradox if we aren't thinking clearly. Here's a simple example: Three persons on a trip agree to share the cost of a room, which is $60, and each pays $20 in cash. Later, the manager realizes that the room is only $55, so the group has been overcharged by $5, which is then given to the bellhop to return. The bellhop realizes it is not possible to divide the $5 evenly, so only $1 is returned to each of the guests, and the bellhop pockets the other $2. Now, if each guest originally paid $20, and they each got $1 back, that would mean they each paid $19 for the room, right? And 3 times $19 gives you $57, plus the $2 the bellhop kept, which now totals $59. So where’s the missing dollar? If you find the fuzzy thinking, here, you should find the missing dollar. We'll leave you with a final apparently paradoxical situation that can arise when a surface is "created" (described mathematically). Sometimes you end up with a surface that encloses a finite volume, but the surface area itself is infinite. Now, how can the same object be both finite and infinite? Discussions of these beasts is often concluded with the amusing, '...so, you can fill it with paint (i. e., the volume is finite, so there's enough paint in the universe to fill it), but you can't paint it (i.e., since the surface area is infinite, it would take an infinite amount of paint to cover it)" What kind of paradox is this? One that melts away on closer examination, or one that forces us to rethink what kind of substance "mathematical paint" might be? For an exploration of this question, see http://fulcrum.org/projects/egems/paint.html |