Pendulum Motion
Pendulum MotionA pendulum is a freely hanging weight that is capable of swinging back and forth. That weight is acted on by gravity, and moves according to Newton's second law which states that an object will accelerate in proportion to the net force acting on it, and inversely proportional to the objects mass. (If you push harder, an object will accelerate faster, if it is more massive, it is harder to push.) This is often written as
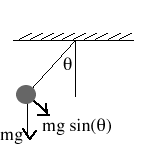
F=ma, the angular versionWhen a pendulum is hanging, the tension in the rope or rod acts against the force of gravity. As a result, only that component of gravity which acts perpendicular to the pendulum rod will accelerate the pendulum.
Notice that as the pendulum moves, the forces always acts along a tangent line to the pendulum's arc. We could then express this motion as
. Note that we are using the angular form of Newton's second law, where the rate of change of the angular momentum is proportional to the net torque. With a little simplification, this can be written as
Small Angle Approximation
This is not an equation with a simple answer we can write on paper.
As a result, scientists often use an approximation known as the
small angle approximation, which states that Under the small angle approximation, the equation for a pendulum becomes
The only functions whose second derivatives are equal to -1 times the original function are the sinusoidal functions sine and cosine. This gives us for the equation of a simple pendulum under the small angle approximation
where the amplitude of the oscillation is given by the initial amount by which the pendulum was displaced, and the frequency given by the square root of g/L. |