Bandpass Filters

The magnitude scale

The magnitude scale historically was simply a ranking system. There was no real standard, other than that the brightest stars were designated as first magnitude stars, slightly dimmer stars were second magnitude stars, then even dimmer stars were third magnitude, and so on.

To make things more rigorous, modern astronomers use a scale where the difference in magnitude between two stars is determined by the ratio of the flux of light from those stars. A magnitude is defined such that an object which is 10 times brighter is two and a half magnitudes lower.

m₂-m₁=-2.5 log₁₀ (F₂/F₁)

When we see magnitudes in astronomy, the measurement is one of a star being dimmer or brighter than something, but what are we comparing it to? We need to have some object with which we measure everything else with respect to. For visual light, this reference is Vega. In practice, a zero magnitude flux is defined for each wavelength region of interest.

Common astronomical bands

Measuring the amount of light at every wavelength is a difficult thing to do. If you have a finite amount of light coming in in different wavelengths, then the more specific you are about the exact wavelength you want, the more you limit yourself. In addition, filtering out light of unwanted wavelengths can be both difficult and expensive. Typically, astronomer have searched for filters that are easily made and replicated that limit the range of wavelengths that can be detected to a small, but not infinitesimally small, range. These regions of wavelength allowed by a given filter are referred to as bands.

The following are the primary wavelengths and zero magnitude fluxes for the UBV bands on the Johnson scale, RI on the Cousins scale, and JHK on the UKIRT scale.

Filter	Primary wavelength (nm)	Zero point flux (Jy)
U	360	1810
B	440	4260
V	550	3640
R	640	3080
I	790	2550
J	1250	1670
H	1650	980
K	2200	620

If a star is giving off light of a given intensity I (often assumed to be blackbody radiation,), the flux of light coming off the star is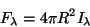

$\begin{displaymath} F_{\lambda} = 4 \pi I_{\lambda} \end{displaymath}$

Notice that the flux as a function of wavelength is not the same as the flux as a function of frequency. The reason for this is that wavelength dependent flux is defined such that the total energy within some wavelength range is conserved. Thus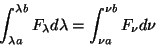

$\begin{displaymath} \int_{\lambda a}^{\lambda b} F_{\lambda} d \lambda = \int_{\nu a}^{\nu b} F_{\nu} d \nu \end{displaymath}$

The zero point magnitudes above are defined in terms of a frequency dependent flux, not a wavelength dependent flux.

CSERD

Bandpass Filters

Bandpass Filters

The magnitude scale

Common astronomical bands