Wave Equation Lesson
Lesson - Wave EquationsIn its simplest form, the wave equation can be expressed as "A restorative force is applied to a medium in proportion to the difference at a point in the medium from its surroundings." If you stretch a rubber band, it rebounds. If you drop a pebble in water, forcing a small region of the water to be lower than its surrounding, the surrounding water rushes in. When this equation is applied to a point mass, we get simple harmonic motion, such as is seen with a mass on a spring or a pendulum swinging with a small angle. When this equation is applied to a larger medium, such as a stretched string, water in a pool, or the air around us, we need to separate the property that is being displaced (such as the height of a vibrating string, or the pressure of air at a point) from the coordinate used to describe locations in the medium. This is where the wave equation in a medium start to look a little different from the equation of simple harmonic motion. In one dimension (such as vibrations on a stretched spring) the wave equation looks like
In multiple dimensions (such as waves on the surface of a pool) the wave equation is written as
Waves on a stringConsider a taut string, such as is modeled in CSERD's 1D Wave Equation model. Just because the elevation of the string changes as we move along the length of the string, that will not in and of itself create a restoring force. If one end is being pulled up while the other is being pulled down, the two will cancel out. We are looking for how the displacement relative to nearby spots on the string changes. If displacement is change in position, and we are concerned about the change in displacement as we move along the string, then we want to look for a change of the change of the position, or the second derivative of the elevation.
The greater the tension (T) of the string, the greater the restorative force.
The greater the density per unit length (
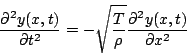
If there is some reason for the string to slow down, such as air resistance, we could put that into this equation as well. Let's assume that the faster the string vibrates, the more air resistance and internal resistance acts to slow the string down. If we define a resistivity r such that the force due to resistance is equal in magnitude to the resistivity times the velocity of the string, we get
where
As the tension of the string is increased, what happens to the motion of the string? The length? The mass? Does the dissipative effect on the string change the frequency of the resulting wave? How is the wave reflected at the other end? Does the sign (wave is above or below the "zero" height of the string) change or stay the same? Does it make a difference if the end of the string is fixed? Can you create a wave that is "stable" (the string just moves up and down, the displacement doesn't appear to "shift" from side to side? How is that stable wave different if one or both ends of the string are fixed? Waves of this sort are called standing waves. How does the shape of this stable wave change if you change the tension of the string? The length? The mass? If you want to try a model of a string with more detail, try the vibrating string model from Paul Falstad's Math and Physics Applets. |



