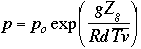
The Javascript calculator to the right will allow you to experiment with the relationships between the variables in the sea level pressure reduction equation below.
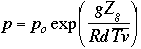
Sample values are supplied to give you a feel for what a "normal" value might be for the variables on the right hang side of the equation. You can go ahead and click on "CALCULATE" to compute the equivalent sea level pressure for the default values. Or, by using the "Reset Values", "Clear Field", and "Clear All" buttons, you can solve for any of the variables listed in the table. Just one note, to ensure an accurate computation, the text field of the variable for which you wish to solve must be blank when you click on "CALCULATE".
The following is a description of each of the variables for which you can solve.
Most (though not all) land surfaces are at some elevation above sea level. Just inland, near the coast, the elevation may be less than a meter above sea level, while the surface of mountainous regions may be thousands of meters above sea level. In this equation, the sea level pressure is the theoretical pressure the air would have if the atmosphere continued below the ground to zero elevation (sea level). If the elevation of the land surface happens to be below sea level, then the surface elevation (above sea level) is considered to be negative and the sea level pressure is the pressure of the atmosphere at sea level.
Normally, the units for pressure must be converted to Pascals (Pa) when performing computations in SI units; however, this calculator requires units of kiloPascals (kPa) and makes the conversion to Pascals for you.
The surface pressure is just that, the actual measured air pressure at the surface, irregardless of the elevation of the surface. This is the pressure that is going to be reduced. The units for surface pressure should also be entered as kPa. For elevations above sea level, the surface pressure is always less than the equivalent sea level pressure. Conversely, for a surface at an elevation below sea level, the surface pressure will always be greater than the sea level pressure.
The acceleration due to gravity is nearly constant around 9.81 m/s2, but because the earth is not perfectly round, this value does vary slightly from place to place. When performing computations, you can either use the default or vary it a little to see the effect it has on the values of the other variables.
The surface elevation is generally referred to as the height above sea level (in meters). However, the actual ground surface elevation could be above or below sea level. Sea level is considered zero elevation. If the ground surface is above sea level, as in most cases, then the surface elevation is a positive number. If the surface elevation is below sea level, then it is considered negative.
Average Virtual Temperature (Tv):
To review, the definition of virtual temperature (Tv) is the temperature to which a sample of dry air must be heated in order to have the same density as a sample of moist air at the same pressure. When reducing the air pressure at a surface above sea level, the reduced pressure is a theoretical pressure. It is the pressure of the air at sea level if the atmosphere continued below the ground to zero elevation. The average virtual temperature referred to here is an estimated theoretical average virtual temperature (in degrees C) of this imaginary layer of air between the ground surface and sea level.
The average virtual temperature of this theoretical layer of air can actually be computed and is a function of the real atmospheric conditions (above the surface) such as the temperature, moisture content, and lapse rate of the air. For our purposes, we do not need to know how to compute this value. We simply need to be able to get a sense of how this variable relates to the others in the equation.
Note:
The gas constant used in this calculation is the gas constant for dry air, 287 J/kgK.