Numerical Weather Prediction: Temperature Advection Calculator

Introduction : This calculator demonstrates an example equation of motion - temperature advection in one direction -- as an example of the type of equations used in numerical weather prediction. This equation is an example of a "finite-difference" equation, which is loosely defined as:

New value = old value + change

For example, In this calculator, you have seven input values:

  1. the potential temperature at the beginning of the forecast (for example, time = 0)
  2. the potential temperature in the box of interest at some change in time (dt) later, in this example at time = 10 minutes
  3. the potential temperature in the "western" box at the latest time
  4. the potential temperature in the "eastern" box at the latest time
  5. the wind speed (U) in meters/sec (changed to km/min automatically by the calculator)
  6. the width of the box in the x-direction (dx), in meters
  7. the time step (dt)

The algorithm for the the cumulative daytime heating is:

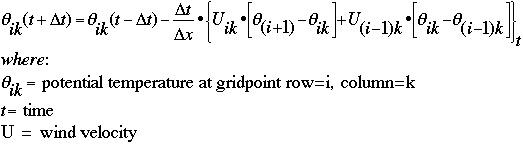
Mathematical equation for temperature advection in one direction

For example, a sample scenario (the one modeled by this calculator) is shown below:

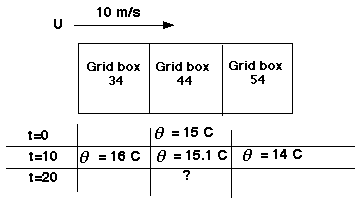
Diagram of grid boxes
In this scenario, we are looking at 10-minute intervals, with the potential temperatures shown in underneath each of the grid boxes. In this schematic, i=3,4, and 5 (moving across from left to right), and k=4. We are interested in forecasting the potential temperature (in degrees C) at time=20 minutes for Gridbox 44. We know that the temperature at t=10 minutes is 15.1 degrees, and we wish to know the temperature 10 minutes later. The windspeed from Gridbox 34 going into 44 is 10 m/s.

In the algorithm above, t= 10 minutes, t+dt= 20 minutes, t-dt = 0 minutes, i=4, k=4.

Temperature Advection Calculator

Input Values:

Potential temperature in Gridbox 44 at t=0
Potential temperature in Gridbox 34 at t=10
Potential temperature in Gridbox 44 at t=10
Potential temperature in Gridbox 54 at t=10
Windspeed in Gridbox 34 (m/s)
Windspeed in Gridbox 44 (m/s)
Size of the box (in x-direction), in meters
Time step, in minutes

Results:

Potential temp at t=20 for Gridbox44