Radiative-Convective Models: Algorithm

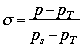By definition, sigma=0 at the top of the column (since you have P_T-P_T), and by definition sigma=1 at the surface (since you have P_s-P_T/P_s-P_T). A simple four-layer model might look like this:

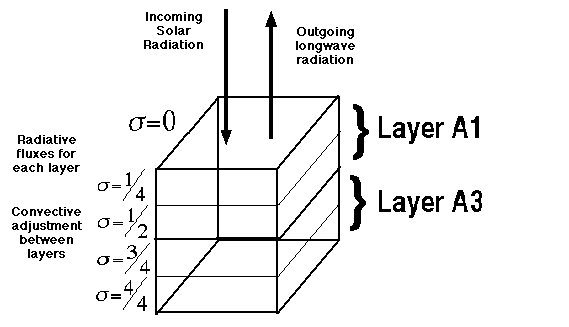In this diagram, we show two layers, A₁ and A₃. In most RC models, the net radiative cooling (a balance of shortwave and longwave radiation) is often shown at the midpoints of two layers, in this case between layers 1/4 and 3/4.

The mechanics of how these models are built is perhaps shown in the graphic below:

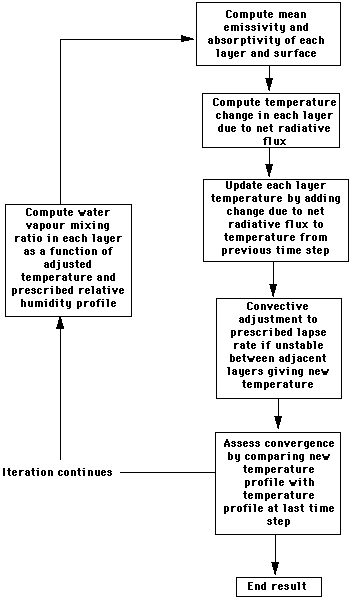The procedure starts with a computation of the amount of radiation emitted and absorbed at the interface of each layer, as well as at the surface. Typically the model starts with an isothermal ("equal temperature") atmosphere, all layers have the same temperature. Dependent on the amount of radiative flux (incoming and outgoing radiation), a change in temperature for a particular layer is calculated. Factors that can affect this net radiative flux are cloud coverage, dust (such as volcanic dust from an eruption), surface albedoes, and other optical properties. Three behaviors can occur in each layer:

• Radiation is absorbed in the layer
• Radiation is transmitted to a layer below or above
• Radiation is reflected back up

Obviously, at the surface there is no transmission, only reflection and absorbtion.

Once the temperature change has been calculated, a simple additive step updates the temperature in each layer by adding the change in temperature to the temperature in the previous timestep. It is helpful to remember that RC models are iterative in nature; that is, they repeat through a time-specific cycle until some stopping condition is met.

At this point the convective portion of the model comes into play. RC modelers state that the layer is "convectively unstable" if the lapse rate for that layer is greater than some predetermined critical lapse rate. Lapse rate is defined as:

... as the rate at which temperature decreases per unit increase in altitude. A steep lapse rate implies a rapid decrease in temperature with height, a sign of instability.For example, if the temperature is 20 degrees C at the surface and 10 degrees C at 2 km altitude, the lapse rate is - (10-20)/(2-0) = 5 degrees C/km. Note that the lapse rate is defined to be positive when the temperature gets colder as one moves upward (the usual state of affairs for Earth's troposphere).