| |
|
Meteorological Models - Algorithm
The MM5 meteorological model uses these basic equations:
- pressure
- momentum (x-, y- and z-components)
- thermodynamics
- advection
- divergence
The model also provides for a variety of other algorithmic decisions. For example, there are a number of physics options, such as:
- cumulus parameterizations
- planetary boundary layer (PBL) schemes
- explicit moisture schemes
- radiation schemes
- ground temperature schemes
Each of these options presents the user with a number of choices. For example, in the physics option Cumulus Parameterizations, there are approximately six different algorithmic options available:
- None: uses no parameterization, useful for grid sizes between 5 and 10 km.
- Anthes-Kuo: good for grid sizes greater than 30 km, an algorithm based on moisture convergence, tends to produce too much convective rainfall in the model runs
|
|
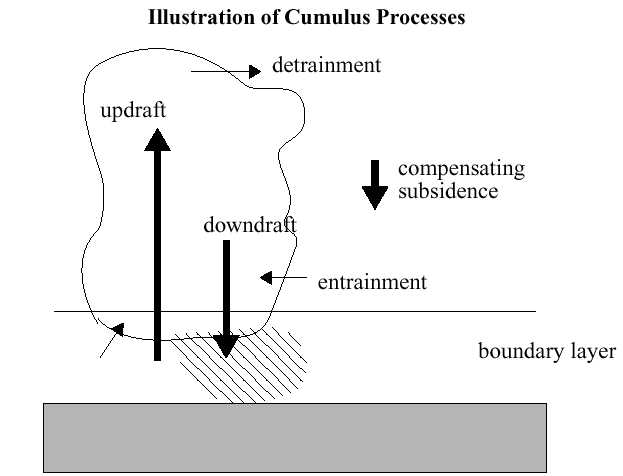
- Grell: useful for grid sizes between 10 and 30 km, considered to be a "multi-cloud" scheme, allowing for updrafts and downdrafts.
- Arakawa-Schubert: good for grid scales greater than 30 km, a multi-cloud scheme like the Grell method. Is considered to be one of the more computationally expensive of the schemes.
- Fritsch-Chappell: good for 20-30 km grid sizes, a single-cloud algorithm, predicts updraft and downdraft properties.
- Kain-Fritsch: a variation on Fritsch-Chappell that uses a sophisticated cloud-mixing algorithm to determine entrainment and detrainment.
- Betts-Miller: an algorithm that works well for grid sizes greater than 30 km.
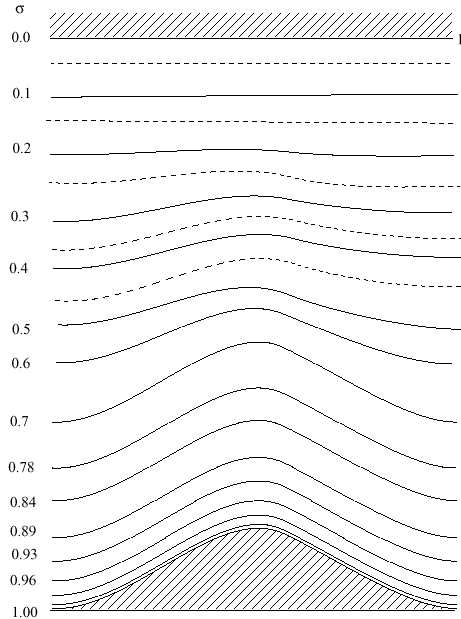
| The graphic at right (click on image to see full-sized) shows the terrain-following vertical layering used by MM5. The sigma levels begin at 1.0 (the surface) and roughly mimic the terrain, at least until the upper layers, where the sigma levels become isobaric. The model can handle up to 40 layers, depending on the value of some specified constant top pressure (pt). The dimensionless value of sigma is determined by this equation:
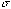 (sigma) =(p -pt)/(ps-pt) (sigma) =(p -pt)/(ps-pt)
where p is the pressure and ps is the surface pressure.
|
|
|
|