| |
|
Puff Models: Algorithms
| Puff models are Gaussian models, following the basic algorithm shown at right. |
|
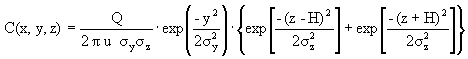
This equation provides an estimate of the downwind puff concentration from a stack having a specific height (H). The variable Q represents the total mass of the release, and the  (sigma) values are the disperson coefficients that follow the motion of the expanding puff. Examples of dispersion coefficients for y and x are shown in the table below:
| Parameter |
Condition |
Downwind Distance |
Downwind Distance |
| (m) |
|
100 m |
4000 m |
| y |
Unstable |
10.0 |
300.0 |
| y |
Neutral |
4.0 |
120.0 |
| y |
Stable |
1.3 |
35.0 |
| x |
Unstable |
15.0 |
220.0 |
| x |
Neutral |
3.8 |
50.0 |
| x |
Stable |
0.75 |
7.0 |
There are a variety of ways in which puff models calculate how puffs grow in size over time and distance. One algorithm modifies the values of sigma using the equation: =axb, where x is the distance traveled, and a and b are growth coefficients that depend on the stability of the atmosphere, using the Pasquill-Gifford stability classes:
| Stability Class |
ay |
by |
ax |
bx |
| A |
0.36 |
0.9 |
0.00023 |
2.10 |
| B |
0.25 |
0.9 |
0.058 |
1.09 |
| C |
0.19 |
0.9 |
0.11 |
0.91 |
| D |
0.13 |
0.9 |
0.57 |
0.58 |
| E |
0.096 |
0.9 |
0.85 |
0.47 |
| F |
0.063 |
0.9 |
0.77 |
0.42
|
A simpler generic algorithm for calculating the concentration of some chemical species X in the puff is given by:
dX/dt = E + P - L - D
where E is the emissions, P is production from chemical processes, L is chemical loss, and D is deposition, all in units of molecules of X per cubic centimeter per second.
|
|
