|
|
Energy Balance Models: Algorithm
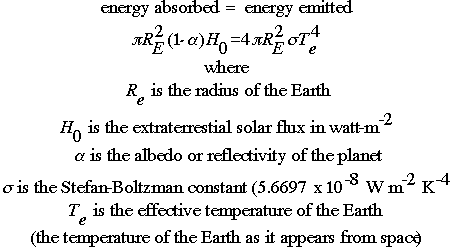 Energy balance models are typically one-dimensional, that dimension being latitude. What we are trying to calculate is the temperature at the surface. The model itself aims to calculate the effective temperature, Te. We are interested in the temperature at the surface, or Ts. The following calculation is used to calculate Ts:
where dT is the greenhouse increment. At this time, the greenhouse increment is about 33 degrees Kelvin, and is a function of the efficiency of the infrared absorption. All this would be fairly simple except for the fact that most energy balance models are not global models, but zonal, or latitudinal, models. As such, we must have some equation or part of an equation that accounts for the flow of energy from one latitudinal zone to the next. The graphic below shows a zonal one-dimensional energy balance model: 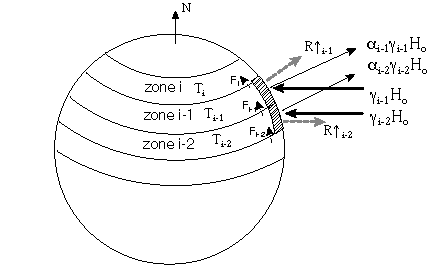 In a simple global energy balance, the only variable is the temperature of the Earth, usually signified as Te. The term "balance" suggests that the system is at equilibrium -- no energy is accumulated. In this schematic, we are showing that the equation has now become:
In the zonal model, we need to be able to calculate the total energy received from the sun per unit time. This is given by:
 R2H0 R2H0
where R is the radius of the Earth and H0 is the solar constant. Given that the Earth's total area can be calculated by 4
where
We also need to consider the fact that not all zones receive the same amount of incoming radiation, since the incident angle of the sun to a particular zone varies. There exists some ratio,
 H0/4 H0/4We are also concerned with the surface albedo of each zone. These are dependent upon the ratio between land and water and the type of land covering. The critical temperature, Tc, is the temperature below which the land becomes ice covered. The typical literature value for this temperature is -10.0 degrees C. For a given zone, the surface albedo depends on the surface temperature of that zone. If the surface temperature is below the critical temperature, the albedo for the zone is the albedo of ice, or 0.68. For temperatures above the critical temperature, several equations are used. The most typical is:
Cloud albedo is typically specified as being 0.5. Fractional cloud cover values are a typical input for a standard energy balance model.
The transport of energy between zones is given by:
where:
Again, the purpose of the energy balance model is to calculate the temperature of the zone. A final equation for calculating temperatures is as follows:

In this equation, Ti represents the temperature of the individual zone, i. This equation is iterated until an equilibrium value is reached, determined by some user-defined tolerance value. The algoritm for another sample EBM model is presented below. In this model, McGuffie and Henderson-Sellers (source: "A Climate Modeling Primer", K. McGuffie and A. Henderson-Sellers, John Wiley and Sons, New York, 1997) present a relatively simple one-dimensional EBM, in which each latitude zone is evaluated independently. The fundamental equation:
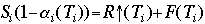 states the energy balance. Solar radiation coming in (Si) times the fraction reflected due to albedo (which is itself dependent on temperature) "balances out" the outgoing radiation (which is temperature-dependent) plus a transport out, or energy loss by a latitude zone to its colder neighbors. The surface albedo, or the amount of incident radiation reflected back to the atmosphere, is, like all of the parameters in the energy balance algorithm, dependent on the surface temperature for a given zone or latitude. In this case, we have simply made the albedo a "toggle" parameter, alternating between two choices if the zonal temperature is more or less than the critical temperature. The critical temperature at which a zone "ices over", or glaciates is:
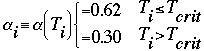 Radiation leaving the zone is calculated by:
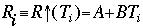 where A and B are longwave radiation loss constants which approximate the greenhouse effects of clouds, water vapor, and carbon monoxide. Energy transport out of the system is a function of a transport constant, K, times the difference between the zonal temperature and the mean global temperature:
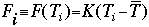 Zonal temperature can be calculated by rearrangment of several of the preceeding equations:
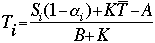
Confused? Have a question? If so, check out the Frequently Asked Questions (FAQ) page or send mail to the OS411 tutor (os411tutor@shodor.org) with your question! Report technical/content problems here |
|
|