Spreadsheets

Spreadsheets are a valuable computational tool in that they are inexpensive and relatively easy to use. In addition, they are becoming more powerful in terms of computing capabilities, data analysis/graphing/visualization capabilities, and ability to write short "programs" to do repeated tasks. Some of the newer generation spreadsheets, (Microsoft Excel, Lotus 1-2-3, and Quattro Pro) are excellent computing tools capable of doing decent scientific work and not just tools for balancing your checkbook.

Spreadsheets use the concept of a "cell", a box which is referenced by its column name (starting with the letter A) and its row number (starting with the number 1). The first cell, for example, is called "A1". Into each cell we can introduce a number, a formula, and/or a built-in function such as pi or square root. Formulas can be easily reproduced for all the cells in a column or row using one of two fill procedures -- a "fill down" or a "fill right".

A familiar example is useful. In this case, we wish to find the value of x in the root equation: x²-4 = 0. To do it, we will use Newton's algorithm, which is an iterative technique involving the current value of x, the value of the function, and the value of the derivative of the function. The problem solved using a spreadsheet is shown below. Notice that the final answer of 2 is reached fairly rapidly.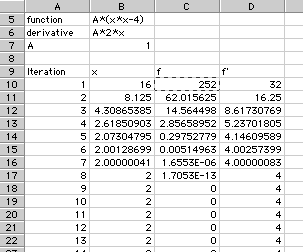

The graphic below shows the underlying formulas for this application. The values near the top are either text labels or single numbers. The working part of the spreadsheet is towards the bottom. The initial value of x comes from cell B3.

The first value of the function is calculated by multiplying this value of x -- in cell C9 -- times itself and then subtracting the 4. Likewise, the derivative is computed by multiplying the initial x in Cell C9 by 2. The next value of x uses Newton's algorithm:

Essentially, this algorithm takes the slope of the function at some "guess" point, and extrapolates to a point where that slope would cross the x-axis. This x-intercept becomes the new guess point, and the process is repeated.

Notice, however, that there are no loop structures in a spreadsheet. You cannot simply say "run until done" or "run 1,000,000 times". Each operation requires a cell to be filled out. Cutting and pasting can make that process fairly painless, but having to keep track of each cell does not make very efficient use of memory. The lack of loops can make handling multidimesional problems especially difficult on a spreadsheet.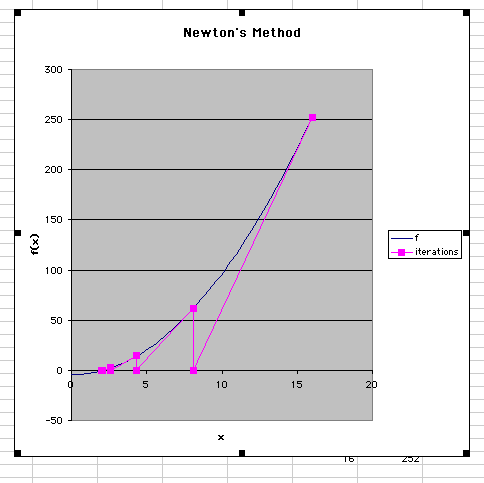

There are a number of tutorials on using spreadsheets (using Excel and other spreadsheets) on the Web. You might consider trying to build several of the models presented in this course using a spreadsheet. Your spreadsheet should have come with a tutorial. You might need to work through it in order to do some of the problems and case studies!