Algorithms

Algorithm is the term used to describe the mathematical representation of a physical event or phenomenon being investigated. Typically in the computational sciences, an algorithm or mathematical model is developed by the investigator, often with the support of a mathematician. Depending on the phenomenon being investigated, a "recipe" is chosen or developed to solve for the mathematical model. In choosing a solution strategy for a mathematical model, computational scientists will often try to first determine if the model can be described with a particular type of mathematics. Examples would be a root equation, an ordinary differential equation, a spline equation, a least-squares equation, or an eigenvalue/eigenfunction equation. If the model can be so classified, there exist numerous methodologies for solving these equations computationally. Indeed, there exists a number of on-line numerical libraries, mostly in the computer programming language FORTRAN, that allow computational scientists to obtain complete codes that can be pasted into computer code that will solve most classes of equations. These libraries substantially decrease the time, effort, and cost needed to obtain a computational solution to a problem. Once you are involved in computational sciences, you will quickly come to understand the heated discussions between FORTRAN programmers and programmers who use a newer language called "C". Certainly one of the reasons why FORTRAN has withstood the changes in computer sophistication is because of the huge number of numerical libraries that are available in FORTRAN.

Examples of libraries of numerical routines are:

• HARWELL (FORTRAN77/90)
• ISML (C, FORTRAN77/90, Java)
• NAG (FORTRAN77/90, C)
• LAPACK (FORTRAN77)

Mathematical models can be quite simple or quite complex. You've been dealing with mathematical models for many years, you just might not have known it! Let's revisit your high school or freshman chemistry class. In all beginning chemistry courses, a study of gas laws -- how gasses behave under a variety of conditions, such as temperature, pressure, and volume. In all likelihood you were presented with the "ideal gas law", which is just a simple mathematical model that attempts to capture the physical behavior of common gasses:

PV=nRT

where P represents pressure, V is volume, n is the number of moles of gas, R is a gas constant, and T is temperature in units of degrees Kelvin. Under most circumstances, this mathematical model is fairly accurate in its prediction of the behavior of common gasses. However, like all mathematical models, it makes some simplifying assumptions that make it possible for the model to include as many different conditions as possible. The assumptions made for this model are as follows:

• the molecules never bump into each other
• under conditions of high pressure, the volume of gas molecules can be compressed down to a volume of zero

Needless to say, these are ridiculous assumptions, but they are accepted since they do allow the model to describe in a very broad sense the relationship between the variables. A question, however, might be: isn't there a mathematical model that can remove these assumptions? The answer, of course, is yes, there are several. The most well-known model that removes these assumptions is the Van derWaals algorithm:

You should notice quickly that this algorithm is substantially more complicated than the Ideal Gas Law, and is probably too rigorous mathematically for use in most beginning or intermediate level chemistry classrooms. You might notice the addition of two new variables, a and b. These values, which are specific for specific gasses, are "fudge factors" that help to take into account the fact that gas molecules DO bump into each other and that they are NOT infinitely compressible.

We want to be able to use this mathematical model as a better representation of the behavior of gasses, especially atmospheric gasses that operate at various extremes of temperature and pressure. Let's construct a hypothetical scenario. Suppose you wish to calculate the volume of a gas such as carbon dioxide, knowing the pressure, temperature, number of moles, and the values of a and b for CO₂. In order to be able to solve this, you need to be able to isolate the variable V (volume) on the lefthand side of the equation, with all of the known variables on the righthand side. If you remember your algebra, take a few minutes to try this. Give up? It so happens that this algorithm is cubic for volume, meaning that V is cubed as a part of the algorithm. It cannot be solved "analytically." That is, it cannot be solved by using traditional algebraic techniques. So, we still need some method to help us solve for volume. If you look at the equation as it is presented above, you should notice that we have all of the variables on the lefthand side of the equation and the equation itself is set to zero. Any equation that is set to zero is known as a "root" equation. We now have a family of equations that we can recognize, and we can go to the mathematical libraries to see if there are any "recipes" for solving root equations. Luckily, there are many such recipes! The most well known is Newton's method. We'll present this method now to help you understand what a numerical method looks like and how we can apply it to a particular type of mathematical model/algorithm/equation.

Let's choose a simpler mathematical model to present Newton's Method. As a lab activity, you will be asked to use Newton's Method to solve the Van derWaals equation. Newton's Method is an iterative method, meaning that we make repeated calculations until some criteria is met, usually some threshold or barrier that we (arbitrarily) set depending on the precision and accuracy of the answer needed. In Newton's Method, the recipe begins by the computational scientist making an intelligent guess, based on physical reality, as to what the right value for the unknown might be. For demonstration purposes, we'll investigate this mathematical model:

X² - 4 = 0

You can probably solve this root equation by inspection: x is either 2 or negative 2. But we want to solve this using the proper methodology. The recipe is as follows:

• Phrase the problem as "some function of x equals zero" f(x)=0.
• Guess a value for the root of the function f(x).
• Calculate the slope of a tangent line to the function f(x) at that value of x.
• Determine where that tangent line crosses the x-axis.
• Use that value of x for the new guess.
• Repeat the process until further iterations don't cause a "significant" change in the guess.

Some simple examples of this can be seen using the Newton Method Calculator. Start with the first function, 0.1*(x-4)*(x-4). Can you use Newton's method to determine the value of the root? How about the other two functions? Notice that the applet starts with an initial guess of 8. Does the initial guess affect the outcome of Newton's method?

Alternatively, we could use a spreadsheet to solve the algorithm (we will discuss spreadsheets and other computing tools in more depth later in the course):

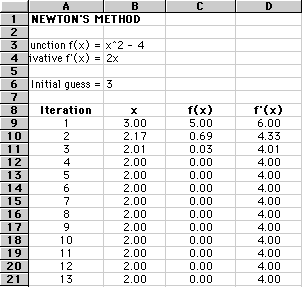You should notice that our choice of a guess converges VERY quickly, after the fourth iteration, and that the answer to the value of the unknown is 2.0. What if, however, we have a really bad guess, like 50?

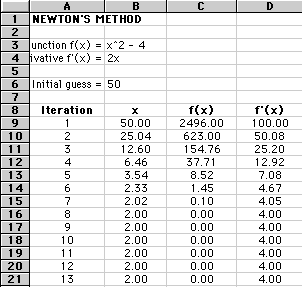In this example, we don't converge until the eighth iteration. There will be some root equations, as you might suspect, that cannot be solved using Newton's, and other more powerful methods then need to be employed. The point is that as a computational scientist you either need to know the methods, know where to find them, or be working with a competent mathematician who does know the methods used to solve equations such as this.

Before we leave this example, you might wish to see the formulas used to build the spreadsheet:

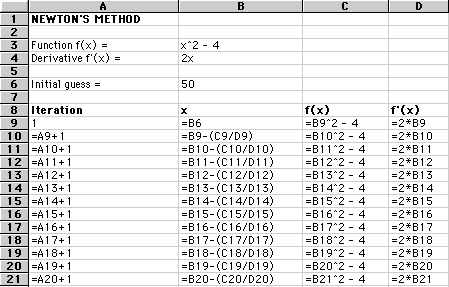[NOTE: If you have access to a spreadsheet and have not used one before, I would recommend that you take some time to look at this models and try to build them yourself.]