Mass Balances
A variety of chemical compounds flow from one location to another in the earth's atmosphere --- from the ocean to the atmosphere, from the soil to the ocean from animals to the oceans, from fossil fuels to the ocean and the atmosphere and so on. The regular flows of material through the earth's atmosphere and surface are known as biogeochemical cycles. Atmospheric cycles of this sort are critical components of atmospheric models. Models become tremendously complex as the modeler considers more and more of the chemical processes that might affect the concentration of the gases and contaminants of interest. The purpose of this unit is to familiarize the reader with some scaled-down versions of atmospheric cycle models as a springboard to the more complex models that will follow. The primary tool used to model the movement of contaminants through a defined volume or mass of air, relies on the principle of mass and energy balances. The law of conservation of mass states that mass can neither be created nor destroyed. Energy is also conserved and cannot be created or destroyed. These physical laws serve as anchor points in computational atmospheric sciencein the form of mass balance and energy balance equations. Mass and energy balance equations permit a sort of accounting system for tracking fairly complex movements of a large number of pollutants throughout the atmosphere. The principle of conservation of mass means that if the amount of a
pollutant in a predetermined volume of air increases, that increase must result either
from a net influx of mass into that volume, or from chemical
transformation due to a chemical reaction involving other chemicals present
in the volume of interest. This can be stated simply in an equation:
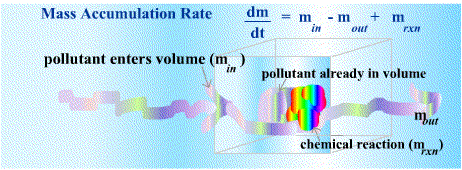 Energy balance equations are used to calculate the amount of energy
entering or leaving a volume of interest and are key to the calculation of
global warming effects. The main idea for energy balance calculations
is analogous to the above example for mass balances.
We can characterize the concept of the atmosphere as a whole as a "system", in this case a closed system. The diagram below shows the sources, sinks, and "fluxes" of this system. Notice that the system is initiated by sources --- motor vehicles, industry, power plants, and other contributors. From these sources, emissions of several types are generated. These emissions then undergo a variety of transformations, some meteorological (dispersion, transport, etc.) and some chemical/physical (oxidation, degradation, etc.). Eventually these constituents cause an impact on receptors, and generate a response in the form of control strategy options (legislation, technical solutions), which should reduce the amount of pollution from the source.
From a detailed knowledge of the emissions, topography, meteorology, and chemistry, we can develop mathematical models that predict the concentrations of primary and secondary pollutants. The predictions can be made as a function of time at various locations in a given air shed. These computer-based models may describe the concentrations in a plume from a specific point source (plume models), in an air basin from a combination of diverse mobile and stationary sources (air shed models), or over a large geographical area downwind from a group of sources (long-range transport models). To validate these models, their predictions must be compared to measured concentrations of the pollutants collected as part of ambient air monitoring programs. Model inputs are adjusted to obtain acceptable agreement between the observed and predicted values. (Source: Finlayson-Pitts, B.J., Pitts, J., Atmospheric Chemistry: Fundamentals and Experimental Techniques, Wiley and Sons, 1986)
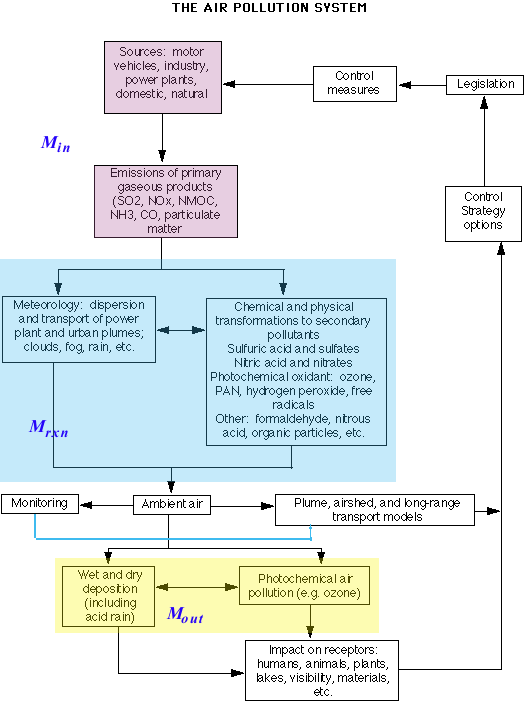 (Source: adapted from Finlayson-Pitts, B.J., Pitts, J., Atmospheric Chemistry: Fundamentals and Experimental Techniques, Wiley and Sons, 1986)
Report technical/content problems here |
|
|