Constant Velocity

When we think of velocity, we usually deal with the average velocity over some time period. The speed of your car on the highway, for example, is 65 miles per hour meaning that if you were to drive at the same speed for 1 hour in a straight line, you will move 65 miles from your starting position. While most physical situations, if looked at in close enough detail, do not occur at constant velocity, it is often a good enough approximation to make useful estimates.

This definition of velocity is often the first we learn, where velocity is equal to distance traveled divided by the time it takes to do so:

For example, consider a drive across a sixty mile stretch of North Carolina which takes the driver 1 hour to complete. The average velocity over the course of the trip is V=D/T, or 60 miles / 1 hour, or 60 miles per hour.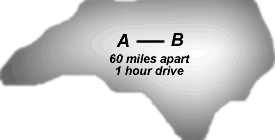

The three main variables we are concerned with when we study the motion of an object are position, velocity (rate of change of position), and acceleration (rate of change of velocity). All of these quantities have both a magnitude and a direction associated with them. In straight line or one dimensional motion, we represent this direction with either a positive or a negative sign. In multiple dimensions, we must represent the direction and magnitude using vectors.

From the standpoint of physics, constant velocity problems are also important because they describe the state of motion one encounters when there are no examples of external forces, or when an environment is in free-fall, such as on the space shuttle in orbit. We will discuss this in more detail when we learn about Newton's Laws.