Enthalpy 

The word enthalpy comes from the Greek "heat inside". If you have a chemical system that undergoes some kind of change but has a fixed volume, the heat output is equal to the change in internal energy (q = DE). We will define the enthalphy change, DH, of a system as being equal to its heat output at constant pressure:

DH =  q             at constant pressure

You will not need to calculate the enthalphy directly.  Chemists are usually interested in the change in enthalphy,  or DH. Tables of enthalphies are widely available and can be used to calculate DH where,

DH = DE + P D V

 DV is the change of volume, and P is pressure, held at a constant value.
 

Since work is defined as PDV, an enthalphy change is simply the amount of energy change (energy going in or out, endothermic or exothermic), plus the amount of work being done by the reaction.
 

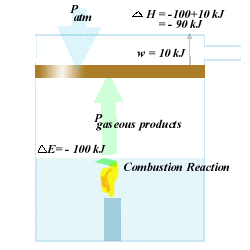
For example, if DE = -100 kJ in a  combustion of a solid,  but 10 kJ of work needs to be done to move a piston so that there is  "space" for the gaseous products, the change in enthalphy is:

DH = -100 kJ + 10 kJ = -90 kJ

This is an exothermic reaction (as you would expect with combustion.), and 90 kJ of energy is released to the environment. 

Notice the convention used here -- a negative value represents energy coming out of the system and being transferred to the surroundings.
 
 

 

Enthalpy is a state function. A state function is a property whose value does not depend on how the change takes place. Your bank balance is a state function. Your balance of $100  is completely unaffected by whether you received the money as a gift in one lump some or earned it for working 10 1-hour shifts. The two paths to the balance are different but the balance remains the same. The internal energy of a system, E, is also a state function.

The value of the state function in determining the change in enthalpy of a system lies in the fact that it is not necessary to know the exact series of chemical reactions that transform reactants to products to determine the enthalpy of a new system.  Any series of reactions that gets you from the reactants to the products will yield the same DH. Hesse's Law is a calculating technique that allows you to apply this insight.
 


The gases CO and NO are pollutants that form in the exhaust of automobiles.  A chemist studying how to convert them to less harmful gases might start with the following equation:

                    CO (g)  +  NO (g)   CO2 (g)  + 1/2 N2 (g)      DH = ??

She has on hand the following related information:

                    Equation A: CO (g)  +   1/2O2 (g)  CO2 (g)         DH = - 283.0 kJ
                    Equation B: N2 (g)  +  O2 (g)   2NO(g)              DH = 180.6 kJ

Perhaps Equations A and B can be manipulated algebraically to yield the "target" equation, the one our chemist is working on.  Then the   DHs for Equations A & B can be summed to give the correct DH for the target equation.

                           reverse Equation B and divide by 2 

         NO(g)  1/2 N2 (g)   + 1/2O2 (g)           DH = - 90.3  kJ

        CO (g)  +  1/2O 2(g)  CO2 (g)          DH = - 283.0 kJ

after cancelling the 1/2O 2 that appears on both sides of the equation and adding the altered equation Equation B to Equation A, she obtains the target equation and the   DH for the target reaction:
 
          NO (g)  +  CO (g)   CO2 (g)  + 1/2 N2 (g)              DH = - 373.3 kJ

Quick Quiz: Which of the following statements about enthalpy is true? 
Since enthalpy is a state function, the overall enthalpy depends only on the enthalpies of the initial and final states.
Change in energy is a state function but enthalpy is not.
A change in enthalpy with a negative sign indicates that an endothermic reaction will occur.
There is no difference between the enthalpy change involved in the formation of liquid water and qas phase water vapor.  

Report technical/Content problems here