Limiting ReactantsThe problem on the previous page assumes that you have exactly the right amount of reactants to combine completely to make the product. It would be the equivalent of baking a cake with only the correctly measured amount of flour and butter and sugar available. It seldom happens that way. You usually buy a 5 pound bag of sugar, take out the 1 cup of sugar required by a recipe and then store the remaining sugar for some future baking project. The same thing happens in chemical reactions. You usually do not start with exactly the right amount of each of the reactants. Some of the reactants will be left over in an unreacted form after all of the other reactants have been used up. This excess reactant does not show up in the chemical equation. You must calculate the amount of each reactant necessary to complete the reaction using the ratios in the balanced equation and stoichiometry. Let's begin with another food analogy. If you want to make s'mores, you would begin by looking at a recipe.
Then you might go to the grocery store to buy the ingredients. Of course, you can't just buy 2 sheets of graham crackers, or 1/2 a bar if chocolate. You might find that you can purchase a package with 20 sheets of graham crackers, a bag with 30 marshmallows and a package with a dozen chocolate bars. How many s,mores can you make from these purchases? The answer is obvious. Since you need two graham crachers per s'more and you have purchased a package with 20 crackers, you can only make 10 s'mores from that package. If you had an infinite supply of graham crackers and marshmallows, you could have made 24 s'mores from your supply of chocolate, and if you had had an infinite supply of crackers and chocolate, you would have been able to make 15 s'mores using your marshmallow supply. But, in this case at least, its the supply of graham crackers that limits your product --- lots of s'mores. The recipe is a lot like a chemical equation. It gives the ratio of the ingredients in the smallest amounts necessary to get a complete s'more. The chemical equation lists the ratio of reactant and products necessary to produce some amount of product. The reactants may be available in large amounts that don't exactly match the ratios in the equation. How can you determine how much product you will actually have? You will use the balanced equation and stoichiometry. Take a look at the following example. 2 Al(s) + 3S(s) 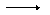 Al2S3(s) Al2S3(s)
Report technical/Content problems here |
|
|