| |
Oxidation-Reduction Reactions
In
oxidation-reduction
(or redox) reactions the main
event of interest is the transfer of one or more electrons from one of
the reactants to the the other. Redox reactions are essential to
life processes like photosynthesis and energy transfer within the body,
the conversion of chemical energy to electrical energy that fuels the modern
world, and many industrial processes. In the atmospheric sciences,
redox reactions play important roles in many biogeological cycles, the
production of pollutants like CO2 that result from fossil fuel
combustion, acid rain production and perhaps most importantly, redox reactions
are at the heart of a variety of photochemical processes in the atmosphere.

Let's try an example. For nitric acid, HNO3, based
on rule number 3 hydrogen has a +1 Oxidation Number and each oxygen atom
has a -2 Oxidation Number. Since there are three oxygen atoms that
is a total Oxidation Number of 3 x -2 = -6 from the oxygen atoms.
-6 + (+1) from the hydrogen atom give an Oxidation Number of -5.
We still have not assigned a number to nitrogen, but since the molecule
must have an overall charge of 0, the nitrogen must have an Oxidation Number
of +5 to balance the Oxidation Numbers of the hydrogen and oxygen atoms.
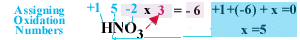
By assigning oxidation numbers to each atom in an equation it is possible
to see which atoms are oxidized, that is lose electrons from the left hand
side of the equation to the right hand side of the equation. Atoms
that are reduced are the atoms that gain electrons from the left hand side
of the equation to the right hand side of the equation.
In the redox
equation shown below Al metal starts out with an oxidation number of 0
since it is in its elemental form. Al in the ionic compound aluminum
sulfate has and oxidation number of +3 meaning that each atom of the metallic Al(s)
lost 3 electrons during this reaction. It was oxidized.
The H in sulfuric acid had an oxidation number of +1 on the left hand side
of the equation, but during the reaction the hydrogen was released as the
diatomic gas, H2. Since this is the elemental form of
hydrogen, the oxidation number went to 0 meaning that each hydrogen atom had gained
one electron. Since it gained an electron it was reduced.

|
Like acid-base reactions, redox reaction are matched sets. Since
these reactions occur as a result of the transfer of electrons you cannot
have oxidation occuring without an accompanying reduction reaction.
The terminology used in to describe these processes is often confusing.
When you first learned about redox reactions you may have come across some
helpful numonics --- LEO GER. "LEO" stands for
lose
electrons: oxidized. "GER" stands for gained electrons: reduced.
Take a look at the table to the left for a summary of redox terminology.
An accounting system has been devised by chemists in which oxidation
numbers (oxidation states) are assigned to each atom according to the following
rules.
General Rules for assigning oxidation numbers:
- 1. For an atom in its elemental form (Na, O2, Cl2
etc.) Oxidation Number = 0
- 2. For a monatomic ion ( Cl-, Na+, Ca2+)
Oxidation Number = ion charge
- 3. The sum of Oxidation Numbers for the atoms in a compound must equal
zero
- 4. The sum of Oxidation Numbers in for the atoms in a polyatomic ion
equals the ion charge
|
Rules for specific atoms or periodic table groups:
For Group 1 Oxidation
Number is +1 in all compounds
- For Group 2 Oxidation
Number is +2 in all compounds
- For hydrogen Oxidation Number
is +1 in all combinations with nonmetals
- -1 in combination with metals and boron
- For flourine Oxidation
Number is -1 in all combinations
- For oxygen Oxidation
Number is -1 in peroxides
- -2 in all other compounds (except with F)
- For Group 17 Oxidation Number
is -1 in combination with metals, nonmetals (except O) and other halogens
lower in the group.
|
|
Notice that when the coefficients for Al and H are worked into the equation,
a total of 6 electrons are lost on the reactant side of the equation
and the same number are gained on the product side of the equation when the oxidation number for a single atom is multiplied by the appropriate coefficient or subscript.
When redox equation are balanced, not only is it necessary to account for
the atoms of each element and balance them on both sides of the equation,
but the number of electrons moving from one side of the equation to the
other must also balance.
In order to track the electron movement and balance an equation it is
useful to divide a redox reaction into 2 half-reactions --- the oxidation
half of the reaction and the reduction half of the reaction.
After each half reaction is balanced, the reaction can be recombined and rebalanced. The electrons on the reaction side must be balanced by an equal number of electrons on the product side in order to finally balance a redox reaction.
For the reaction between Cu(s) and AgCl(aq) here is an example of the half reactions redox balancing method.
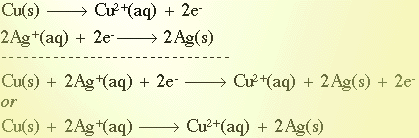
Notice the use of the net ionic form of the equation to balance the equation. The spectator ions, 2 Cl-(aq), are left out since they do not contribute anything to the reaction. The final balanced equation would be:
Cu(s) + 2 AgCl(aq)  CuCl2 + 2 Ag(s) CuCl2 + 2 Ag(s)
If you would like to experiment with the redox reactions, take a look at the redox calculator.
Cu(s) + HNO3(aq)  Cu(NO3)2(aq) + NO2(aq) + H2
O (l) Cu(NO3)2(aq) + NO2(aq) + H2
O (l)
Report technical/Content problems here
|
|
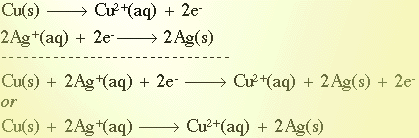
 CuCl2 + 2 Ag(s)
CuCl2 + 2 Ag(s) Cu(NO3)2(aq) + NO2(aq) + H2
O (l)
Cu(NO3)2(aq) + NO2(aq) + H2
O (l)