Vector Analysis: Degrees and Radians
The two most common units of measuring angles are degrees and radians. Most calculators will let you choose which you want to work with, but you need to be sure your calculator is set correctly, or the results of trigonometric functions will be incorrect.
Consider a pie broken up into 360 equal slices. This is much like the unit of degree (o), which measures the size of an angle in portions of 1/360th of a full circle.
The radian is defined such that if your have a circle of radius r, the arc length subtended by an angle of 1 radian is r. This makes it easy to convert from angle to arclength. Unfortunately, it doesn't let us break up the pie evenly. So, we break up the pie into two pieces of pi (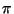 ), so to speak.
), so to speak. 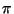 is defined as the number of radians in an angle of 180o. This means there are 2
is defined as the number of radians in an angle of 180o. This means there are 2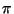 radians in a 360o angle (or a full circle). The value of
radians in a 360o angle (or a full circle). The value of 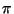 cannot be expressed exactly, but it is approximately 3.14159. When writing angle measures in radians, typically no unit is written, that is, the statement that
cannot be expressed exactly, but it is approximately 3.14159. When writing angle measures in radians, typically no unit is written, that is, the statement that 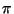 radians is equal to 180o is generally written as
radians is equal to 180o is generally written as 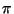 = 180o.
= 180o.
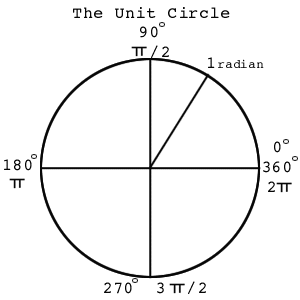
To convert from degrees to radians, multiply by 180o/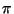 .
.
To convert from radians to degrees, multiply by 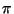 /180o.
/180o.
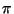 ), so to speak.
), so to speak. 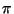 is defined as the number of radians in an angle of 180o. This means there are 2
is defined as the number of radians in an angle of 180o. This means there are 2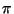 radians in a 360o angle (or a full circle). The value of
radians in a 360o angle (or a full circle). The value of 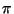 cannot be expressed exactly, but it is approximately 3.14159. When writing angle measures in radians, typically no unit is written, that is, the statement that
cannot be expressed exactly, but it is approximately 3.14159. When writing angle measures in radians, typically no unit is written, that is, the statement that 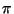 radians is equal to 180o is generally written as
radians is equal to 180o is generally written as 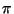 = 180o.
= 180o.
